Can Bootstrap Resampling be used to Calculate a Confidence Interval for the Variance of a Data Set?
Yes, just as with many other statistics.
I know that if you re-sample from a data set many times and calculate the mean each time, these means will follow a normal distribution (by the CLT).
It is not always the case that if you bootstrap a mean the bootstrap means will follow a normal distribution, even for distributions for which the CLT applies.
Here's an example where I resampled the mean for a sample of size $n=100$, where I resampled 10000 times:

It's not remotely normal.
The original sample consists of ninety-seven '0' values, and a '1', a '2' and a '100'.
Here's the (R) code I ran to generate the plot above:
x <- c(rep(0,97),1,2,100)
y <- replicate(10000,mean(sample(x,replace=TRUE)))
plot(table(y),type="h")
The problem is that in this case the sample size (100) is too small for the CLT to apply with this sort of distribution shape; it doesn't matter how many times we resample it.
However, if the original sample size is much larger, the resampling distribution of sample means for something like this will be more normal-looking (though always discrete).
Here are the ecdfs when resampling the above data (black) and for values in the same proportions but with ten times as many values (red; that is, n=1000):
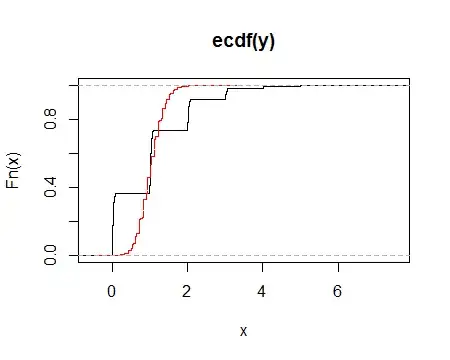
As we see, the distribution function when resampling the large sample does look much more normal.
if I were to re-sample from a data set many times and calculate the variance each time, would these variances follow a certain distribution
No, for the same reason it's not necessarily true for the mean.
However, the CLT does also apply to the variance*; it's just that you can't argue that the CLT applies to bootstrap resampling simply by taking many resamples. If the original sample size is sufficiently large, that may (under the right conditions) tend to make the resampling distribution of means (and higher moments, if they exist) relatively close to a normal distribution (relative to its distribution in smaller samples, at least).
* that the CLT usually applies to the variance (assuming appropriate moments exist) is intuitive if you consider $s_n^2 = \frac{1}{n}\sum_{i=1}^n (x_i-\bar x)^2$. Let $y_i = (x_i - \bar x)^2$; then $s_n^2 = \bar y$, so if the CLT applies to the $y$-variable, it can be applied to $s_n^2$. Now $s_{n-1}^2$ is just a scaled version of $s_n^2$; if the CLT applies to $s_n^2$ it will apply to $s_{n-1}^2$. This outline of an argument is not completely solid, however, and there are some exceptions that you might not expect at first.

