What is the probability that a person will die on their birthday?

Question

I am curious about what the probability is that a person will die on their birthday?

I am sure there are a number of ways to approach this, plus I have heard that actual numbers point to a higher rate on birthdays, hence why I am asking it here.

Answer 1

Sorry, a bit new here so please excuse me if this doesn't help too much.

The US Social Security Administration keeps records of births and deaths and has their information available for purchase (apparently for a hefty price): Here

However I found a source that claims to have bought it and is offering it for free (as well as offering the data sorted by date on the site): Here

I'm assuming you can just use that as your sample and go through all the data with a script and find how many people actually die on their birthday. I would do that myself but I have 20 min left to download (they're about 1.5GB) so I'll try to get back to you on the statistics myself if I find the time to write up a script.

Of course the United States can't represent the entire world's population but it is a good start. I'm assuming you will see a higher rate in deaths on birthdays because of "first world problems" because we're using the United States and I think the effect would be less visible across the world...

Update - Numbers :D

I've ran through the Social Security Death Master File from the free source, so there's no way knowing if the information is valid. However, given the size that they're ~3 Gigabytes each and that there's no reason for anyone to spoof these kind of files... I'll assume they are valid.

You can see the code that I used to run through it here: http://pastebin.com/9wUFuvpN

It's written in C#, it reads through the lines of the death index one by one and then parses the date using regex. I assumed that the file was basically this format:

`(Social Security Number)(First Name)   (LastName)   (Middle Name)    (Some Letter)(MM-DD-YYYY of Death)(MM-DD-YYYY Of Birth)`

I had regex just pick out the last part for the dates of birth/death, check if any of the fields are just 0 (which I'm assuming it means that Social Security couldn't get a valid month/date for the record), and discard the 0's. Then it'll check if the day of birth and month of birth match the day of death/month of death and add that to the died on birthday count. It'll add all records that aren't 0's to the death count.

It outputs the results in this format:

Deaths On Birthday/Total Deaths Lines Looked Through - People With a 0 in any of their record

It's be great if someone could double check that code, as I've found quite a few errors I've made before and could only tell because my results made no statistical sense.

Here is the console output: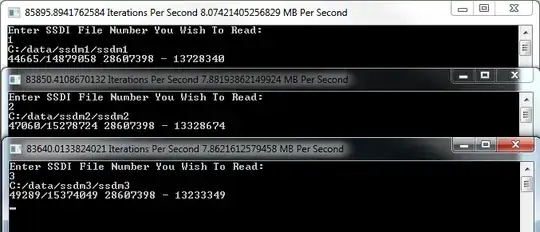

Doing some math...

• File 1 had 44665 Deaths on a Birthday out of 14879058 Deaths in Total
• File 2 had 47060 Deaths on a Birthday out of 15278724 Deaths in Total
• File 3 had 49289 Deaths on a Birthday out of 15374049 Deaths in Total
• Total we have 141014 Deaths on a Birthday out of 45531831.

So we have ~0.3097% chance of dying on a birthday while statistically (1/365) would lead us to believe there is only ~0.27397% chance of dying on a birthday. That is indeed a 13% increase in chance of death on a birthday from 1/365. Of course this sample is only for Americans and only has 45 million records, I'm sure organizations who originally published their paper had access to much more reliable and larger death indexes. However, I think that it is indeed valid that deaths on a birthday is more likely than death on any other day.

Here's a Time article citing jumps in reasons for death on birthdays: Article

Edit 2: @cbeleites pointed out that I forgot to account for same day deaths, which would be a huge factor in increasing deaths on birthdays. Strictly speaking my data is still valid but I did not throw out if a person died on the same day they were born. It's interesting that my results were not affected too heavily by this error so it seems that these records don't include death on first day. I'll look into it later. I'm thinking there would be very interesting statistics I can look for such as death on days of the month and make a heatmap of some sort. I'll probably try to do that sometime...

Answer 2

We can be even more precise than @Mike Shi's data: the most dangerous of all birthdays is the very first one.

The 1st day mortality rates reported there are around 0.2 % for industrialized countries and 0.8 % average for all countries. Which means that the risk of dying on the day of birth is at least as high as the risk of dying at any of the following birth days*.

* I think it is a safe assumption that 1st day deaths do not appear in @Mark Shi's file, as the US 1st day mortality rates are reported to be 0.3 % (other source: 0.26 %). Which is almost the total birth day death rate in the social security file. So either babies who die at the day of birth do not get a social security number, or dying on a birth day > 1 year is extremely improbable.

---

side note:
There are other days, such as Chirstmas and New Years Eve which are known to have higher-than-average mortality rates as well.

Answer 3

Here's an argument why the probability of death on the birthday may be higher than on other days: Birthdays are emotionally charged days. More over, people tend to celebrate it somehow.. So there is an excess of factors (relative to the person's usual life style) that increase biological stress (excess emotions, excess drinking, excess eating, excess dancing, excess banjee jumping etc). Statistically speaking, this situation increases the chances of dying on a birthday, since it intensifies any health issues a person may have, or because it exposes the person to situations and risks for which the person is inexperienced.

Answer 4

In addition to the other excellent answers, but there is a point none of them discussed: Birthdays are not uniformly distributed over the year, and neither are deathdays. That conspires such that the "statistical" probability is not 1/365. To get an idea of this effect, lets first assume they are both almost uniform, only 29 february has a probability 1/4 of the others. That gives $$ 365 p + \frac14 p=1 $$ so $p= 0.002737851$. That leads to probability of birth and death on the same day equal $356\cdot p^2 + (p/4)^2= 0.002736445 > 0.00273224=\frac1{366}$ which is the minimum possible value (with 366 days).

With a bit more generality, let $p_i, i=1, \dotsc, n$ be the birthday probabilities, and $q_i, i=1,\dotsc,n$ the deathday probabilities, for a year with $n$ days. Then, if birthday and deathday for a person are statistically independent, we will find that $$ \DeclareMathOperator{\P}{\mathbb{P}} \P(\text{Birth and death on same day}) = \sum_{i=1}^n p_i q_i $$ so if $p_i=q_i$ then that is $\sum_i p_i^2$. That is a quantity known (in biology) as Simpsons index of (bio)diversity. Its inverse could then be taken as "effective number of days (in a year)"! The minimum value of $\sum_i p_i^2$ is $1/n$. To see that use convexity.

But assuming $p_i=q_i$ is quite a stretch, lets first look at some data, birthday probabilities for Norway calculated from data from ssb.no:

Clearly not uniform, the high outlier is 1. july. That is not real, it is caused by immigrants without documented birthday registered that date. One max in spring, around beginning of april, another maximum in autumn, in september. The simpson index calculated from this is $ 0.002750224$, and the inverse is $363.6067$, so the "effective number of birthdays" is about 363 and a half, rather close to 366. So the nonuniformity maybe is not to important. It is more difficult to find data for deathday, but I found the paper (in norwegian) (this is the official journal of the Norwegian medical association) they report around 12% higher rate of death in winter than in summer. They also report a slightly increased risk of death at Mondays! In fact, international comparisons reported by that paper shows that winter overmortality is lowest in scandinavia, in countries like Irland or England it is about double. That might be surprising, might have to do with us Scandinavians having warmer and better isolated houses?

From that we can reconstruct a deathday distribution. I take winter halfyear as november-april. Then we can calculate $$ p_w =1.12 p_s \\ (182 \cdot 1.12 + 184) p_s = 1 $$ leading to $p_s=0.002578383, p_w= 0.002887789$ and finally $\sum_i p_i q_i = 0.00273151$, its inverse, the "effective number of days" being 366.1, pretty close to 366! The anticorrelation ($\rho(p_i,q_i)=-0.06$) seems to offset the nonuniformity in such a way that we could as well assume uniformity (and equal distribution for birthday and deathday). That is quite interesting.

EDIT: Here is a published paper on nonuniformity in the birthday problem.

Answer 5

The probability that a newborn dies within a year can be found in the life tables. For example, you can check out the periodic life tables and look at the column $q_x$ for $x=0$ in the human mortality database. This is not exactly want you want, but will give you an idea.

Answer 6

1 out of 365 would be the correct odds, because you are guaranteed to die on one day out of a 365 day year... Therefore odds are 1 out of 365.