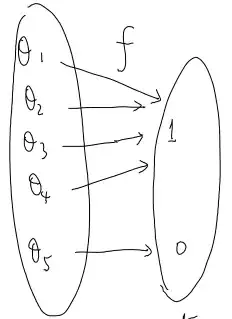
You seem to be confusing what it means for a parameter transformation to occur. In general, the values of the likelihood functions do not change. To illustrate, let $L(\theta; x)$ be a likelihood function and let $\lambda = g(\theta)$ where $g$ is one-to-one. Then the likelihood function parameterized in terms of $\lambda$ is
$$L^*(\lambda; x) = L(g^{-1}(\lambda) ;x) = L(\theta;x)$$
Some trouble occurs when we want to use a function that isn't one-to-one for $g$. In that case we define the likelihood function parameterized in terms of $\lambda$ through the use of profile likelihood as:
$$L^*(\lambda; x) = \sup_{\theta: g(\theta) = \lambda} L(\theta; x)$$
Using these definitions in your example, if $L(\theta_5;x) = 0.4$ then $L^*(0;x) = 0.4$ as well and the actual likelihood values do not change. We also see that $g(\theta_5) = 0$ so there does not appear to be any contradiction. I'll leave the general proof that the MLE is invariant to any parameter transformations up to the interested reader.