I frequently read that Bonferroni correction also works for dependent hypotheses. However, I don't think that is true and I have a counter example. Can somebody please tell me (a) where my mistake is or (b) whether I am correct on this.
Setting up the counter example
Assume we are testing two hypotheses. Let $H_{1}=0$ is the first hypothesis is false and $H_{1}=1$ otherwise. Define $H_{2}$ similarly. Let $p_{1},p_{2}$ be the p-values associated with the two hypotheses and let $[\![\cdot]\!]$ denote the indicator function for the set specified inside the brackets.
For fixed $\theta\in [0,1]$ define \begin{eqnarray*} P\left(p_{1},p_{2}|H_{1}=0,H_{2}=0\right) & = & \frac{1}{2\theta}[\![0\le p_{1}\le\theta]\!]+\frac{1}{2\theta}[\![0\le p_{2}\le\theta]\!]\\ P\left(p_{1},p_{2}|H_{1}=0,H_{2}=1\right) & = & P\left(p_{1},p_{2}|H_{1}=1,H_{2}=0\right)\\ & = & \frac{1}{\left(1-\theta\right)^{2}}[\![\theta\le p_{1}\le1]\!]\cdot[\![\theta\le p_{2}\le1]\!] \end{eqnarray*} which are obviously probability densities over $[0,1]^{2}$. Here is a plot of the two densities
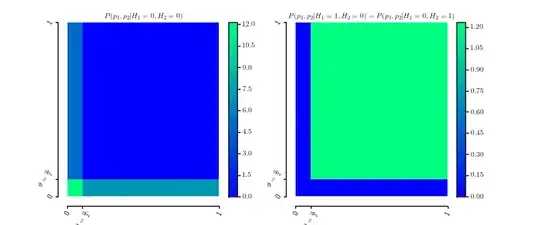
Marginalization yields \begin{eqnarray*} P\left(p_{1}|H_{1}=0,H_{2}=0\right) & = & \frac{1}{2\theta}[\![0\le p_{1}\le\theta]\!]+\frac{1}{2}\\ P\left(p_{1}|H_{1}=0,H_{2}=1\right) & = & \frac{1}{\left(1-\theta\right)}[\![\theta\le p_{1}\le1]\!] \end{eqnarray*} and similarly for $p_{2}$.
Furthermore, let \begin{eqnarray*} P\left(H_{2}=0|H_{1}=0\right) & = & P\left(H_{1}=0|H_{2}=0\right)=\frac{2\theta}{1+\theta}\\ P\left(H_{2}=1|H_{1}=0\right) & = & P\left(H_{1}=1|H_{2}=0\right)=\frac{1-\theta}{1+\theta}. \end{eqnarray*} This implies that \begin{eqnarray*} P\left(p_{1}|H_{1}=0\right) & = & \sum_{h_{2}\in\{0,1\}}P\left(p_{1}|H_{1}=0,h_{2}\right)P\left(h_{2}|H_{1}=0\right)\\ & = & \frac{1}{2\theta}[\![0\le p_{1}\le\theta]\!]\frac{2\theta}{1+\theta}+\frac{1}{2}\frac{2\theta}{1+\theta}+\frac{1}{\left(1-\theta\right)}[\![\theta\le p_{1}\le1]\!]\frac{1-\theta}{1+\theta}\\ & = & \frac{1}{1+\theta}[\![0\le p_{1}\le\theta]\!]+\frac{\theta}{1+\theta}+\frac{1}{1+\theta}[\![\theta\le p_{1}\le1]\!]\\ & = & U\left[0,1\right] \end{eqnarray*} is uniform as required for p-values under the Null hypothesis. The same holds true for $p_{2}$ because of symmetry.
To get the joint distribution $P\left(H_{1},H_{2}\right)$ we compute
\begin{eqnarray*} P\left(H_{2}=0|H_{1}=0\right)P\left(H_{1}=0\right) & = & P\left(H_{1}=0|H_{2}=0\right)P\left(H_{2}=0\right)\\ \Leftrightarrow\frac{2\theta}{1+\theta}P\left(H_{1}=0\right) & = & \frac{2\theta}{1+\theta}P\left(H_{2}=0\right)\\ \Leftrightarrow P\left(H_{1}=0\right) & = & P\left(H_{2}=0\right):=q \end{eqnarray*} Therefore, the joint distribution is given by \begin{eqnarray*} P\left(H_{1},H_{2}\right) & = & \begin{array}{ccc} & H_{2}=0 & H_{2}=1\\ H_{1}=0 & \frac{2\theta}{1+\theta}q & \frac{1-\theta}{1+\theta}q\\ H_{1}=1 & \frac{1-\theta}{1+\theta}q & \frac{1+\theta-2q}{1+\theta} \end{array} \end{eqnarray*} which means that $0\le q\le\frac{1+\theta}{2}$.
Why it is a counter example
Now let $\theta=\frac{\alpha}{2}$ for the significance level $\alpha$ of interest. The probability to get at least one false positive with the corrected significance level $\frac{\alpha}{2}$ given that both hypotheses are false (i.e. $H_{i}=0$) is given by \begin{eqnarray*} P\left(\left(p_{1}\le\frac{\alpha}{2}\right)\vee\left(p_{2}\le\frac{\alpha}{2}\right)|H_{1}=0,H_{2}=0\right) & = & 1 \end{eqnarray*} because all values of $p_{1}$ and $p_{2}$ are lower than $\frac{\alpha}{2}$ given that $H_1=0$ and $H_2=0$ by construction. The Bonferroni correction, however, would claim that the FWER is less than $\alpha$.