2

I read a journal article, in which the authors made a diagram based on regression results (beta weights). Pretty much looks like a path analysis:
I'm very sure that path analysis/SEM was not employed as can be read from their paper:

Both logistic regression and multiple regression analyses were used. Logistic regression was used for the prediction of condom use because the dependent variable was dichotomous. Prediction of the two intention variables was accomplished using multiple regression. This has the advantage over logistic regression of providing estimates of the effect size.

Is that OK? I'm not trying to judge the quality of the paper. On the contrary, if that practice is acceptable, I would like to use it in my paper. I wanted to do path analysis, but I'm afraid my sample size (66 subjects) is too small for that analysis, so I used regression instead.

Nick Stauner
  • 11,558
  • 5
  • 47
  • 105
Simon
  • 21
  • 2
  • 2
    Thanks Andre Silva for your response. Here is the link [link] (http://postimg.org/image/vd6ltakm9/) Thank you very much! – Simon Dec 19 '13 at 01:52
  • While I haven't read the paper, the intermediate variable of "intention in action" makes me laugh. Why not add a couple more such variables? We could attribute what happens in between intention and behavior to the stars, say, or chakras or auras. The possibilities are endless. – rolando2 Dec 19 '13 at 19:42
  • @Simon: I've edited in your comments, and interpreted your first on mtreg's as a quote of the paper – please correct me if that was wrong. If you could provide a reference for the paper itself, that would help too. – Nick Stauner Feb 22 '14 at 12:40

3 Answers3

2

It is a bit tough to discern what is going on without looking at the actual paper, but that appears to be from a Path Analysis or Structural Equation Model, where parameters are estimated for direct and indirect effects of variables on one-another. I tried to find the paper via google scholar, and while I don't have access to the journal, I saw in the abstract that it is examining the theory of planned behavior, for which I understand Structural Equation Modeling is often used.

A great text on structural equation modeling is Principles and Practice of Structural Equation Modeling by Rex B. Kline.

If you search for this method, you might also want to look up the phrase "confirmatory factor analysis".

In doing this analysis, effectively, multiple sets of regressions are run to analyze the relationships between the connected predictor variables themselves, and between the predictor variables and the dependent variable, along the different paths in the model. Thus, the coefficients presented are not simply regression coefficients from a single multiple logistic regression on the entire dataset, as might be inferred from the figure caption. The methodology jibes with what is shown in the figure, and makes logical sense given the information presented and the field that this paper is from.

I hope that helps a bit at least.

mtreg
  • 184
  • 7
  • Thank you very much for your answer. You even tried to find more info through Google Scholar. I really appreciate it. However, I'm very sure that path analysis/SEM was not employed as can be read from their paper: Both logistic regression and multiple regression analyses were used. Logistic regression was used for the prediction of condom use because the dependent variable was dichotomous. Prediction of the two inten- tion variables was accomplished using multiple regression. This has the advantage over logistic regression of providing estimates of the effect size. – Simon Dec 19 '13 at 07:07
  • This is the data that was used in the diagram: http://postimg.org/image/5f6plell3/ – Simon Dec 19 '13 at 07:11
  • By the way, I'm not trying to judge the quality of the paper. On the contrary, if that practice is acceptable, I would like to use it in my paper. Thank you. – Simon Dec 19 '13 at 07:14
  • Thanks for the clarification and posting that table. I was thinking that this paper may have been a bit early in the application of formal path analysis/SEM... But, they were effectively trying to do the same thing. If you have a similar dataset with these hypothesized directional relationships between variables, SEM or Path might be the best and most defendable approach, as there is enough literature available to use as a reference for yourself and to defend your analyses – mtreg Dec 19 '13 at 15:26
  • Sorry - ran out of time on editing previous comment. This link/PDF might help:[link] (http://psych.unl.edu/psycrs/942/q2/pathex1.pdf). If you have a similarly structured dataset, with hypothesized linear relationships among vars., perhaps just explicitly use Path/SEM as it is certainly defendable with enough literature out there to justify your work and to guide you along. – mtreg Dec 19 '13 at 15:32
  • Thank you. Actually I wanted to do path analysis, but I'm afraid my sample size (66 subjects) is too small for that analysis, so I used regression instead. – Simon Dec 20 '13 at 04:46
  • @Simon - Sorry - I don't have any straight-up answer for you then. I guess I would follow guidelines for Path Analysis, and see what you can do - perhaps there are variables that you could condense into a compound variable or something... – mtreg Dec 20 '13 at 19:45
1

I think it's insane.

In theory, I could run any set of univariate (or multiple) regressions and then arrange them any way I please.

While the individual relationships may have been estimated, there is absolutely no evaluation of whether I have then arranged them correctly - i.e. there is no actual test of the theory.

Also, doing it this way ignores the random error in the endogenous variables.

Fortunately, you could, with certain assumptions, use a structural equation model, to estimate all of these regressions in one model, and then evalaute whether the covariance matrix implied by that model is reasonably similar to the observed covraiance matrix.

D L Dahly
  • 3,663
  • 1
  • 24
  • 51
  • @D L Dahly, Thank you. Actually I wanted to do path analysis, but I'm afraid my sample size (66 subjects) is too small for that analysis, so I used regression instead. – Simon Dec 20 '13 at 04:45
1

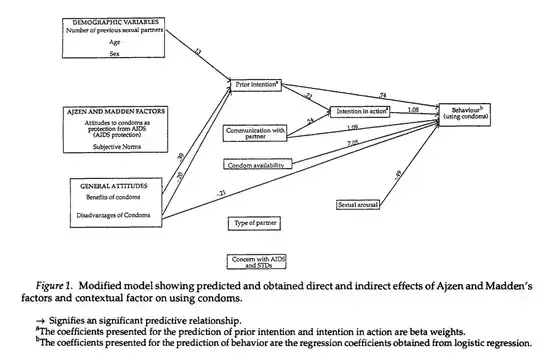
The diagram appears to represent a path analysis. A convention in such diagrams is to represent latent variables with circles, and measured variables with rectangular boxes. If latent variables were involved, this would be a structural equation model; since there is no indication that these variables were not measured directly (using a simply summed/averaged scale score basically counts as a direct measurement of the latent variable it represents via classical test theory), it does appear to be a path model, of which Wikipedia says this (with no particular reference cited, unfortunately):

Path analysis can be viewed as a special case of structural equation modeling (SEM) – one in which only single indicators are employed for each of the variables in the causal model. That is, path analysis is SEM with a structural model, but no measurement model.

FWIW, two lines in Wikipedia's SEM page corroborate the above statement, and I don't see any particular reason to argue with it.

I see from your comments that you're concerned about the use of logistic regression in the final step of the path analysis. This is not a problem. Traditional path analysis proceeds step-by-step in predicting endogenous (dependent) variables, beginning with those predicted by exogenous (purely independent) variables (with no inbound arrows, as with the three sets of variables on the left of your diagram). The first set of endogenous variables can then be used to predict other endogenous variables in subsequent steps involving separate regression analyses to construct a path model. I.e., the logistic regression can be performed after the first two OLS regressions predicting prior intention and intention in action. Modern modeling software can fit the entire model all at once, provide model fit statistics, and accommodate combinations of dichotomous and continuous DVs.

Those fit statistics provide you information about whether your model fits the data sufficiently, as @DLDahly finds lacking in this figure. In its defense, the presence of unconnected measures in this model (e.g., Azjen and Madden factors) suggests the authors attempted to use them as predictors in some way that isn't reflected in the figure itself – but hopefully is in the paper – to test their hypothesized model. Indeed, any set of regressions can be run and arranged as desired, but this is not a problem for purely exploratory research. If a particular, hypothesized model is to be tested, one should report the results for that model – the arrangement of which is not arbitrary – and distinguish these results from any exploratory post-hoc model tweaking. Furthermore, random error in endogenous variables can be identified at each step by noting the fraction of unexplained variance $(1-R^2)$ in each regression model if these are performed separately, or will be identified as the variance estimate for the endogenous variables if the entire model is fit all at once, so it is not ignored necessarily, though this figure does not include this information. Omission of insignificant pathways and error estimates is unfortunately common in SEM reporting, as figures tend to get cluttered quickly.

I also see you're concerned about sample size. Rules of thumb vary regarding recommendations for the minimum number of observations per parameter estimate: I've seen 5, 10, even 20 per estimate recommended. Hence with $n=66$, you could stand a halfway decent chance of fitting 3–13 parameters, depending partly on the quality of your model and the reliability of your measures. I wouldn't tell you not to at least try, but I might recommend crossing your fingers! You never really know what kind of model you can fit until you try (though with really big ones, you can be pretty sure that a small sample = bad news).

Plenty more advice for SEM could be offered depending on the nature of your data (cf. Regression testing after dimension reduction, Factor analysis of questionnaires composed of Likert items), but I'll just offer one more suggestion. One useful alternative for fitting path models with small datasets is partial least squares (PLS) regression. If you're not predicting any one DV with too many IVs, that will help reduce your sample size requirements, because power depends more on that than the overall number of parameters estimated for PLS (Marcoulides, Chin, & Saunders, 2009; Chin & Newsted, 1999). PLS modeling software is freely available through SmartPLS BTW. It can be a little tricky to set up at first, but I've used it myself; it's not half bad!

References

- Chin, W. W., & Newsted, P. R. (1999). Structural equation modeling analysis with small samples using partial least squares. In R. Hoyle (Ed.), Statistical Strategies for Small Sample Research (pp. 307–341). Thousand Oaks, CA: Sage Publications.
- Marcoulides, G. A., Chin, W. W., & Saunders, C. (2009). A critical look at partial least squares modeling. MIS Quarterly, 33(1), 171–175. Retrieved from http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.217.4520&rep=rep1&type=pdf.

Community
  • 1
Nick Stauner
  • 11,558
  • 5
  • 47
  • 105