4

I am studying about Graphical Models and I came up with a simple example but I am not sure which kind of technique (HMM, DGM, MRF) would be able to help me with that.

Imagine we have three balls that can move along this one dimensional space. I can only measure their coordinates:

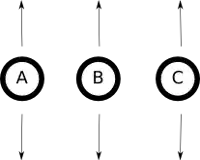
enter image description here

I collect some observations through time and I notice that A always move together with B, in other words, A is correlated with B:

enter image description here

What I would like Graphical Models to tell me is that $A ⫫ C$ (independent) but A and B are not, there is a dependence with them. Moreover, would it be possible to estimate B given that I only measured A? In short:

  • Is it possible to find which Random Variables are dependent (and which ones are not) given only their observations over time t? (e.g. coordinates)
  • Given that I solved the previous problem and I now know which ones have dependence. Assuming also that at a certain time $t_k$ some variables are not observed, how can I estimate the location of a non-observed variable (such as B) given that I observed a dependent a variable A?

I created some possible observations for this example. If somebody could show me concretely how I compute that, it would be great:

A,B,C
0,0,0
0,0,5
1,1,5
3,3,3
2,2,5
4,4,0
2,2,0

So, when I query what is the position of B given that A is 6? How can I use the previous observations to come up with a solution?

Thank you

Sam Felix
  • 148
  • 8
  • Do you want to test for dependence or just correlation? If dependence, then this question is related: http://stats.stackexchange.com/questions/25132/what-is-a-reasonable-independence-test-for-a-time-series/25137#25137 – Neil G Feb 02 '14 at 23:06
  • Dependence. What I wanted to do is to learn the graph from data. I thought about calculating Pearson correlate coefficient between all pairs of variables and use a threshold on those coefficients to decide if they are dependent or not, but it does not sound like a correct solution. Thanks for the link. – Sam Felix Feb 04 '14 at 10:49
  • I think there is a number of issues here. First HMM's as the name suggests are used to model hidden states of a system, your system seems to contain 3 observable states. Second, if you are interested in discovering structure of models, it's feasible but non-trivial, see http://www.openmarkov.org/docs/tutorial/tutorial.html#toc-Chapter-2 for a nice explanation. Third, a graphical model is merely an encoding of a dependency structure. At one point you will have to assume a probability distribution somewhere. If prediction is your goal, you better get it right, or use some other algorithm - nnet. – means-to-meaning Feb 06 '14 at 21:46

1 Answers1

0

If I understood your question correctly, you are looking for algorithms of learning structure of Bayes network.

There are many techniques to deal with the problem, and most of them do actually rely on linear relations between variables (correlation), but not limited to it. Another scores used are: joint likelihood (usually assuming normality), posterior, information criteria (BIC, AIC).

The best algorithm would be to try any possible graph on your variables, and choose the one giving you the best joint score. But of course for most tasks it is not really possible, so many "greedy" methods were developed to find locally optimal solution. Some of them are: Grow-Shrink, Hill Climbing, and more advanced ARACNE, MMPC. Also have a look at the comparison of different methods.

If you are using R, I would suggest you to have a look at the package called bnlearn - it has implementations of all the above mentioned algorithms and is very well-documented and easy to use.

Dmitry Laptev
  • 2,859
  • 21
  • 15
  • Thank you! That was precisely what I wanted. Your answer helps me solving my first bullet. Do you have any hints on my second bullet? Once I "obtain" the structure of the graph and lose of one of the nodes... How can I best estimate that node's location based on the remainder of my graph? – Sam Felix Feb 09 '14 at 19:00
  • @SamFelix exactly the same package helps you to estimate the parameters of your model (method fit), and as soon as you estimated all the parameters you have the conditional distribution for unobserved variable, so you can estimate it's value with the mean (method predict). – Dmitry Laptev Feb 09 '14 at 19:15