Equations in the news: Translating a multi-level model to a general audience

Question

The New York Times has a long comment on the 'value-added' teacher evaluation system being used to give feedback to New York City educators. The lede is the equation used to calculate the scores - presented without context. The rhetorical strategy appears to be intimidation via math:

The full text of the article is available at: http://www.nytimes.com/2011/03/07/education/07winerip.html

The author, Michael Winerip, argues that the meaning of the equation is beyond the capacity of anyone other than, um, Matt Damon to understand, much less an average teacher:

"The calculation for Ms. Isaacson’s 3.69 predicted score is even more daunting. It is based on 32 variables — including whether a student was “retained in grade before pretest year” and whether a student is “new to city in pretest or post-test year.”

Those 32 variables are plugged into a statistical model that looks like one of those equations that in “Good Will Hunting” only Matt Damon was capable of solving.

The process appears transparent, but it is clear as mud, even for smart lay people like teachers, principals and — I hesitate to say this — journalists.

Ms. Isaacson may have two Ivy League degrees, but she is lost. “I find this impossible to understand,” she said.

In plain English, Ms. Isaacson’s best guess about what the department is trying to tell her is: Even though 65 of her 66 students scored proficient on the state test, more of her 3s should have been 4s.

But that is only a guess."

How would you explain the model to a layperson? FYI, the full technical report is at:

http://schools.nyc.gov/NR/rdonlyres/A62750A4-B5F5-43C7-B9A3-F2B55CDF8949/87046/TDINYCTechnicalReportFinal072010.pdf

Update: Andrew Gelman offers his thoughts here: http://www.stat.columbia.edu/~cook/movabletype/archives/2011/03/its_no_fun_bein.html

Answer 1

Here's one possibility.

Assessing teacher performance has traditionally been difficult. One part of this difficulty is that different students have different levels of interest in a given subject. If a given student gets an A, this doesn't necessarily mean that teaching was excellent -- rather, it may mean that a very gifted and interested student did his best to succeed even despite poor teaching quality. Conversely, a student getting a D doesn't necessarily mean that the teaching was poor -- rather, it may mean that a disinterested student coasted despite the teacher's best efforts to educate and inspire.

The difficulty is aggravated by the fact that student selection (and therefore the students' level of interest) is far from random. It is common for schools to emphasize one subject (or a group of subjects) over others. For example, a school may emphasize technical subjects over humanities. Students in such schools are probably so interested in technical areas that they will receive a passing grade even with the worst possible teacher. Thus the fraction of students passing math is not a good measure of teaching -- we expect good teachers to do much better than that with students who are so eager to learn. In contrast, those same students may not be interested at all in arts. It would be difficult to expect even from the best teacher to ensure all students get A's.

Another difficulty is that not all success in a given class is attributable to that class's teacher directly. Rather, the success may be due to the school (or entire district) creating motivation and framework for achievement.

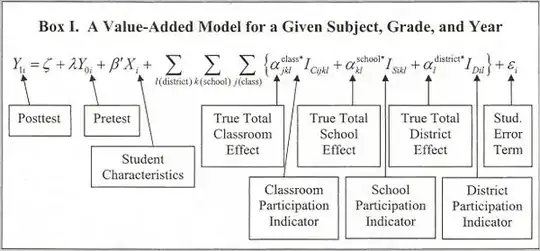
To take into account all of these difficulties, researchers have created a model that evaluates teacher's 'added value'. In essence, the model takes into account the intrinsic characteristics of each student (overall level of interest and success in learning), as well as the school and district's contributions to student success, and predicts the student grades that would be expected with 'average' teaching in that environment. The model then compares the actual grades to the predicted ones and based on it decides whether teaching was adequate given all the other considerations, better than adequate, or worse. Although the model may seem complex to a non-mathematician, it is actually pretty simple and standard. Mathematicians have been using similar (and even more complex) models for decades.

To summarize, Ms. Isaacson's guess is correct. Even though 65 of her 66 students scored proficient on the state test, they would have scored just the same even if a dog were their teacher. An actual good teacher would enable these students to achieve not merely 'proficient', but actually 'good' scores on the same test.

---

At this point I could mention some of my concerns with the model. For example, the model developers claim it addresses some of the difficulties with evaluating teaching quality. Do I have enough reasons to believe them? Neighborhoods with lower-income population will have lower expected 'district' and 'school' scores. Say a neighborhood will have an expected score of 2.5. A teacher that will achieve an average of 3 will get a good evaluation. This may prompt teachers to aim for the score of 3, rather than for a score of, say, 4 or 5. In other words, teachers will aim for mediocrity rather than perfection. Do we want this to happen? Finally, even though the model is simple mathematically, it works in a way very different from how human intuition works. As a result, we have no obvious way to validate or dispute the model's decision. Ms. Isaacson's unfortunate example illustrates what this may lead to. Do we want to depend blindly on the computer in something so important?

---

Note that this is an explanation to a layperson. I sidestepped several potentially controversial issues here. For example, I didn't want to say that school districts with low income demographics are expected to perform poorer, because this wouldn't sound good to a layperson.

Also, I have assumed that the goal is actually to give a reasonably fair description of the model. But I'm pretty sure that this wasn't NYT's goal here. So at least part of the reason their explanation is poor is intentional FUD, in my opinion.

Answer 2

"Your teaching score depends on how well your students did compared to a prediction made based on

• What they knew beforehand, as measured by a pretest,

• How well we think the students can learn based on what we know about them individually (their "characteristics"),

• And how well students do on average in your district, school, and classroom (if there are other teachers in your classroom).

"In other words, we are evaluating you based on the amount of learning that was measured, after factoring in the preparation and characteristics of your students and the typical performances of all students in settings like yours with the resources that were available to you.

"In this way your score reflects what you contributed to the student performances, insofar as we can determine that. Of course we cannot know everything: we know you had unique and special students and that the situation you faced could never be duplicated. Therefore we know this score is only an estimate that imperfectly reflects how well you taught, but it is a fairer and more accurate estimate than one based solely on post testing or on raw test gains made by your class."

Answer 3

There is just nothing to understand here.

Well, ok, it is just a standard linear regression model. It assumes that the score of a student can be described as a linear function of several factors, including school and teacher efficiency coefficients -- thus it shares all the standard problems of linear models, mainly the fact that it is a great approximation of a nonlinear world and may as well work perfectly or embarrassingly bad depending on a situation and on how far one would try to extrapolate with it. (However one should expect the authors of the tech rep checked it and found out that it's ok ;-) ).

But the real problem is that this is an analytical tool and such shouldn't be used to assess people achievements -- this way (totally regardless if the marks are fair or not) every evaluee trying to understand her/his mark (probably in hope of optimizing it) will only meet hopeless confusion, as in this case.