4

Suppose I want to model dependence between $d$ r.v.´s $Y_1,...,Y_d$ with the copula $C_\theta$, where $\theta$ are the corresponding parameters of that copula. I've also determined the correlation using Kendall's tau $\tau(Y_i,Y_j)=\gamma$ for all $i\neq j$. Now I want to generate samples from this joint distribution:

Am I on the right track when I say that, from Sklar's Theorem, we have that if $Y_k$'s corresponding distribution function is $G_k(y_k)$ and we have $X_1,...,X_d$ with distribution functions $F_1(x_1),...,F_d(x_d)$. Then $\bf{Y}$$=\left(G_1^{-1}(F_1(X_1)),...,G_d^{-1}(F_d(X_d))\right)$. So say for example that I want to generate samples of our t-distributed random vector $\bf{Y}$ from the join distribution using a Gaussian copula, I could just simply generate the normal random variables $Y_1,...,Y_d$ (independent) and then apply the t distribution function on the r.v. and then take the normal quantile function of that, using the $\Sigma$ where $$\Sigma_{i,j}=\begin{cases} 1, & \text{if $i=j$}.\\ sin(\frac{\pi}{2}\gamma), & \text{otherwise}. \end{cases}$$ as one of the parameters. Or should the dependence be taken into account for when I model the t-distributed vector $\bf{Y}$? I guess the first makes more sense since the copula is supposed to "model the dependence".

Say instead I want to do the same using the copula package in R. Is it correct to first create the copula object with $\Sigma$ (as before) using normalCopula and then mvdc and rmvdc to generate the samples? But what are the parameters for the mvdc function? The example code from R's web page gives the following:

mvdc(normalCopula(0.75), c("norm", "exp"),list(list(mean = 0, sd =2), list(rate = 2)))

But shouldn't the argument in the normalCopula function be a 2x2 matrix since its bivariate. Also, say now that I have $d$ equally t-distributed r.v.'s and I dont want to write c("t", .... ,"t") etc. How can I write this neatly?

As you can see I'm slightly confused about the parameters in the copula and in what step the correlation should be used (I'm also not sure when it is eligible to say that $\rho = sin(\frac{\pi}{2}\tau)$), so if someone could help clarifying that I'd be very thankful. Also, there are lots of examples of 2-dimensional (and some on 3-dimensional) examples of this on the internet since they are more illustrative than for higher dimensions. So if someone have references to examples of modelling with copulas in higher dimensions in R I would gladly accept that.

Edit:

Ok, say I want to model the joint distribution of two financial assets where the marginals are t-distributed with 3 degrees of freedom and standard deviation 0.05. Their correlation is estimated with $\tau(Y_1,Y_2)=0.5$ I've assumed their joint distribution should be normal, so I use a normal copula. To generate samples from their joint distribution. I first generate samples from the normal distribution:

X<-rmvnorm(N,mu,S) #mu is zero vector and #S is as $\Sigma$ before with $\gamma = 0.5$.

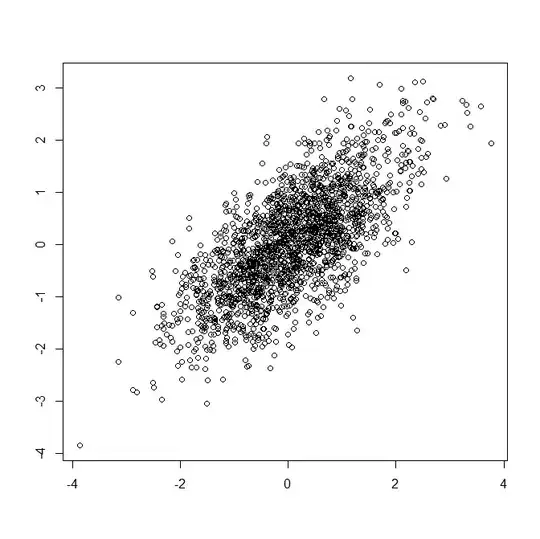
Sample from Multivariate Normal Distr

Now I transform each sample point $(X_k^1,X_k^2)$:

Y<-qt(pnorm(X),df=3)

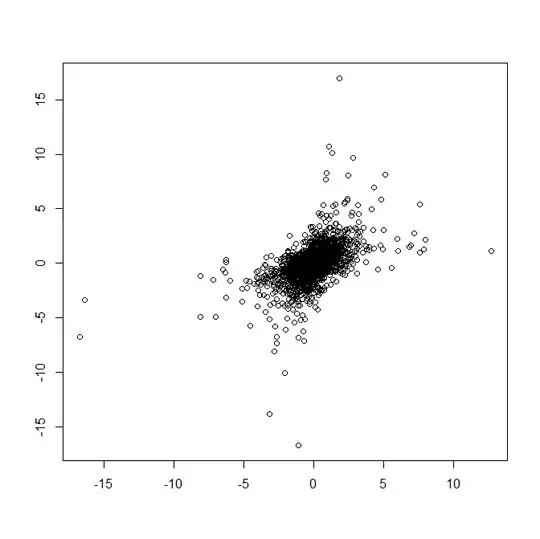
enter image description here

Is this correct? But how do I control the variance/standard deviation of the marginals? Do I do that when I generate the multivariate normal or in the qt function?

Good Guy Mike
  • 611
  • 9
  • 22
  • "*shouldn't the argument in the normalCopula function be a 2x2 matrix since its bivariate*" --- no, the copula is determined by the correlation alone, which for a bivariate is a single value. The additional information in a covariance matrix relates only to the marginals, which don't impact the copula at all. – Glen_b Dec 08 '13 at 02:26
  • 2
    To generate a Gaussian copula with t-margins, the easy way is to generate a multivariate normal, transform to uniform margins (giving the copula) then transform to t-margins. – Glen_b Dec 08 '13 at 09:55
  • Comment #1: Yes that is true, but how is the input constructed if I have higher dimensions, say $d$? Should it then be a (d-1)x(d-1) matrix? Comment #2: I see, so it's as in my first examples the other way around? So I generate the normally distributed r.v. $\bf{X}^d$ with parameters $\mu$ and $\Sigma$ (as in my question). And then I transform it using $\Phi_{\mu,\Sigma}$, and then I apply $g_{\mu^g,\Sigma^g,\nu}^{-1}$ to that? (g is the distriubtion function of my student t distr. r.v's) – Good Guy Mike Dec 08 '13 at 10:26
  • Since the correlations below the diagonal are repeated above it, the structure in a Gaussian copula would be defined by the $d-1\choose 2$ elements in the lower triangular part below the diagonal of the correlation matrix. On the second question, you transform the marginals by their individual marginal distributions (or inverses) in each case. – Glen_b Dec 08 '13 at 15:11
  • I understand that the elements are the same in the lower triangular matrix as in the upper triangular. I didn't understand your notation though. The input is just a vector? I edited my question, could you please look if I understood it correctly. Also, did you know how I could neatly insert the argument in the mvdc function if I have d equally distributed marginals? Without having to write c("t","t","t",.... ) etc. – Good Guy Mike Dec 08 '13 at 17:58
  • "*The input is just a vector?*" -- Sorry, I didn't understand that your question in comments just up there was meant to be "what are the correct inputs for this R function?", something my comments do not address. I haven't read the help on the R functions you mentioned. What do they say about their inputs? How do their examples work? – Glen_b Dec 08 '13 at 20:35
  • Ok, I see. I thought you were talking about the R function in particular. But I think that's fine then. Would you mind commenting on my updated question/example do see if I understood you correctly. Especially about the standard deviation. – Good Guy Mike Dec 08 '13 at 22:07

0 Answers0