14

I'm studying about Student's t-distribution and I started to wonder, how would one derive the t-distributions density function (from wikipedia, http://en.wikipedia.org/wiki/Student%27s_t-distribution):

$$f(t) = \frac{\Gamma(\frac{v+1}{2})}{\sqrt{v\pi}\:\Gamma(\frac{v}{2})}\left(1+\frac{t^2}{v} \right)^{-\frac{v+1}{2}}$$

where $v$ is the degrees of freedom and $\Gamma$ is the gamma function. What is the intuition of this function? I mean, If I look at the binomial distribution's probability mass function, it makes sense to me. But t-distributions density function makes no sense at all to me...it is not intuitive at all at first sight. Or is the intuition just that it has a bell-shaped curve and it serves our needs?

Thnx for any help :)

Glen_b
  • 257,508
  • 32
  • 553
  • 939
jjepsuomi
  • 5,207
  • 11
  • 34
  • 47
  • 3
    This distribution has a simple (and pretty) geometric interpretation. Indeed, although Student (1908) first derived this form of the PDF through an intelligent guess (supported by Monte-Carlo simulation), Fisher (c. 1920) first obtained it with a geometric argument. The essence is that $f$ describes the distribution of the ratio of the *height* of a (uniformly distributed point) on the $\nu+1$-sphere and its *radius* (distance from the axis): in other words, the tangent of its latitude. One account of this is provided at http://www.evolvedmicrobe.com/Literature/GeometricTDistribution.pdf. – whuber Dec 03 '13 at 14:28

2 Answers2

10

If you have a standard normal random variable, $Z$, and an independent chi-square random variable $Q$ with $\nu$ df, then

$T = Z/\sqrt{Q/\nu}$

has a $t$ distribution with $\nu$ df. (I'm not sure what $Z/Q$ is distributed as, but it isn't $t$.)

The actual derivation is a fairly standard result. Alecos does it a couple of ways here.

As far as intuition goes, I don't have particular intuition for the specific functional form, but some general sense of the shape can be obtained by considering that the (scaled by $\sqrt \nu$) independent chi-distribution on the denominator is right skew:

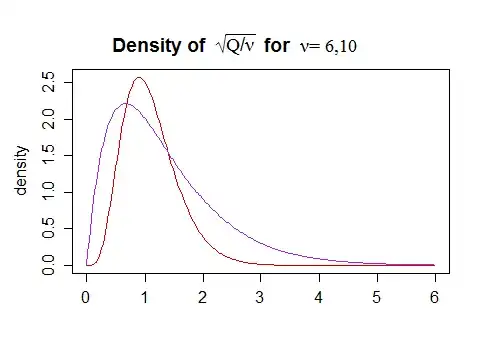
enter image description here

The mode is slightly below 1 (but gets closer to 1 as the df increases), with some chance of values substantially above and below 1. The variation in $\sqrt{Q/\nu}$ means that the variance of $t$ will be larger than that of $Z$. The values of $\sqrt{Q/\nu}$ substantially above 1 will lead to a $t$-value that's closer to 0 than $Z$ is, while the ones substantially below 1 will result in a $t$-value that's further from 0 than $Z$ is.

All this means that $t$ values will be (i) more variable, (ii) relatively more peaked and (iii) heavier tailed than a normal. As the df increases, $\sqrt{Q/\nu}$ becomes concentrated around 1, and then $t$ will be closer to the normal.

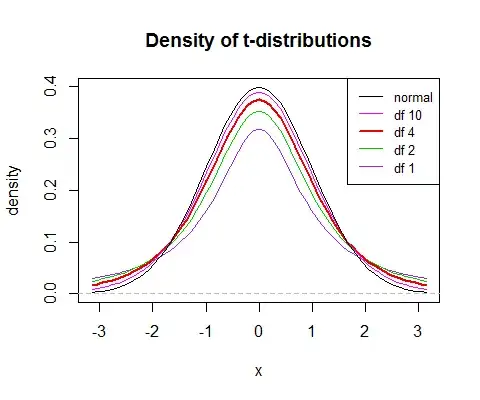
enter image description here

(the 'relatively more peaked' results in a slightly sharper peak relative to the spread, but the larger variance pulls the center down, which means that the peak is slightly lower with lower d.f.)

So that's some intuition about why the $t$ looks as it does.

Community
  • 1
Glen_b
  • 257,508
  • 32
  • 553
  • 939
  • 1
    I was bit sloppy in my explanation. Of course it was square root of Chi-square distributed random variable divided by its degrees of freedom. – Analyst Dec 03 '13 at 08:25
  • @Analyst I've done the same myself, more than once. – Glen_b Dec 03 '13 at 08:31
10

The answer by Glen is correct one, but from a Bayesian viewpoint it is also helpful to think of the t-distribution as a continuous mixture of normal distributions with different variances. You can find the derivation here:

Student t as mixture of gaussian

I feel that this approach helps your intuition because it clarifies how the t-distribution arises when you don't know the exact variability of your population.

Community
  • 1
Erik
  • 6,909
  • 20
  • 48
  • 2
    I've made an animation of the t distribution as a mixture of normal distributions here: http://sumsar.net/blog/2013/12/t-as-a-mixture-of-normals/ – Rasmus Bååth Dec 06 '13 at 20:42