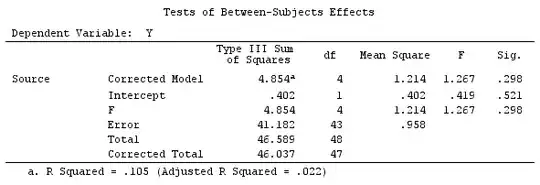
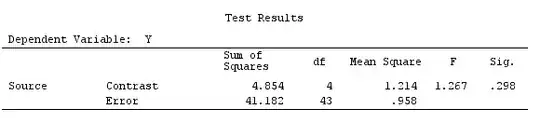
I'll use lower-case letters for vectors and upper-case letters for matrices.
In case of a linear model of the form:
$$
\mathbf{y}=\mathbf{X} \boldsymbol{\beta} + \boldsymbol{\varepsilon}
$$
where $\bf{X}$ is a $n \times (k+1)$ matrix of rank $k+1 \leq n$, and we assume $\boldsymbol{\varepsilon} \sim \mathcal N(0,\sigma^2)$.
We can estimate $\hat{\boldsymbol{\beta}}$ by $(\mathbf{X}^\top\mathbf{X})^{-1}\mathbf{X}^\top \mathbf{y}$, since the inverse of $\mathbf{X}^\top \mathbf{X}$ exists.
Now, take an ANOVA case in which $\mathbf{X}$ is not full-rank anymore. The implication of this is that we don't have $(\mathbf{X}^\top\mathbf{X})^{-1}$ and we have to settle for the generalized inverse $(\mathbf{X}^\top\mathbf{X})^{-}$.
One of the problems of using this generalized inverse is that it's not unique. Another problem is that we cannot find an unbiased estimator for $\boldsymbol{\beta}$, since
$$\hat{\boldsymbol{\beta}}=(\mathbf{X}^\top\mathbf{X})^{-}\mathbf{X}^\top\mathbf{y} \implies E(\hat{\boldsymbol{\beta}})=(\mathbf{X}^\top\mathbf{X})^{-}\mathbf{X}^\top\mathbf{X}\boldsymbol{\beta}.$$
So, we cannot estimate an unique and unbiased $\boldsymbol{\beta}$. There are various approaches to work around the lack of uniqueness of the parameters in an ANOVA case with non-full-rank $\mathbf{X}$. One of them is to work with the overparameterized model and define linear combinations of the $\boldsymbol{\beta}$'s that are unique and can be estimated.
We have that a linear combination of the $\boldsymbol{\beta}$'s, say $\mathbf{g}^\top \boldsymbol{\beta}$, is estimable if there exists a vector $\mathbf{a}$ such that $E(\mathbf{a}^\top \mathbf{y})=\mathbf{g}^\top \boldsymbol{\beta}$.
The contrasts are a special case of estimable functions in which the sum of the coefficients of $\mathbf{g}$ is equal to zero.
And, contrasts come up in the context of categorical predictors in a linear model. (if you check the manual linked by @amoeba, you see that all their contrast coding are related to categorical variables).
Then, answering @Curious and @amoeba, we see that they arise in ANOVA, but not in a "pure" regression model with only continuous predictors (we can also talk about contrasts in ANCOVA, since we have some categorical variables in it).
Now, in the model $$\mathbf{y}=\mathbf{X} \boldsymbol{\beta} + \boldsymbol{\varepsilon}$$ where $\mathbf{X}$ is not full-rank, and $E(\mathbf{y})=\mathbf{X}^\top \boldsymbol{\beta}$, the linear function $\mathbf{g}^\top \boldsymbol{\beta}$ is estimable iff there exists a vector $\mathbf{a}$ such that $\mathbf{a}^\top \mathbf{X}=\mathbf{g}^\top$.
That is, $\mathbf{g}^\top$ is a linear combination of the rows of $\mathbf{X}$.
Also, there are many choices of the vector $\mathbf{a}$, such that $\mathbf{a}^\top \mathbf{X}=\mathbf{g}^\top$, as we can see in the example below.
Example 1
Consider the one-way model:
$$y_{ij}=\mu + \alpha_i + \varepsilon_{ij}, \quad i=1,2 \, , j=1,2,3.$$
\begin{align}
\mathbf{X} = \begin{bmatrix}
1 & 1 & 0 \\
1 & 1 & 0 \\
1 & 1 & 0 \\
1 & 0 & 1 \\
1 & 0 & 1 \\
1 & 0 & 1
\end{bmatrix} \, , \quad \boldsymbol{\beta}=\begin{bmatrix}
\mu \\
\tau_1 \\
\tau_2
\end{bmatrix}
\end{align}
And suppose $\mathbf{g}^\top = [0, 1, -1]$, so we want to estimate $[0, 1, -1] \boldsymbol{\beta}=\tau_1-\tau_2$.
We can see that there are different choices of the vector $\mathbf{a}$ that yield $\mathbf{a}^\top \mathbf{X}=\mathbf{g}^\top$: take $\mathbf{a}^\top=[0 , 0,1,-1,0,0]$; or $\mathbf{a}^\top = [1,0,0,0,0,-1]$; or $\mathbf{a}^\top = [2,-1,0,0,1,-2]$.
Example 2
Take the two-way model:
$$ y_{ij}=\mu+\alpha_i+\beta_j+\varepsilon_{ij}, \, i=1,2, \, j=1,2$$.
\begin{align}
\mathbf{X} = \begin{bmatrix}
1 & 1 & 0 & 1 & 0 \\
1 & 1 & 0 & 0 & 1\\
1 & 0 & 1 & 1 & 0 \\
1 & 0 & 1 & 0 & 1
\end{bmatrix} \, , \quad \boldsymbol{\beta}=\begin{bmatrix}
\mu \\
\alpha_1 \\
\alpha_2 \\
\beta_1 \\
\beta_2
\end{bmatrix}
\end{align}
We can define the estimable functions by taking linear combinations of the rows of $\mathbf{X}$.
Subtracting Row 1 from Rows 2, 3, and 4 (of $\mathbf{X}$):
$$
\begin{bmatrix}
1 & \phantom{-}1 & 0 & \phantom{-}1 & 0 \\
0 & 0 & 0 & -1 & 1\\
0 & -1 & 1 & \phantom{-}0 & 0 \\
0 & -1 & 1 & -1 & 1
\end{bmatrix}
$$
And taking Rows 2 and 3 from the fourth row:
$$
\begin{bmatrix}
1 & \phantom{-}1 & 0 & \phantom{-}1 & 0 \\
0 & 0 & 0 & -1 & 1\\
0 & -1 & 1 & \phantom{-}0 & 0 \\
0 & \phantom{-}0 & 0 & \phantom{-}0 & 0
\end{bmatrix}
$$
Multiplying this by $\boldsymbol{\beta}$ yields:
\begin{align}
\mathbf{g}_1^\top \boldsymbol{\beta} &= \mu + \alpha_1 + \beta_1 \\
\mathbf{g}_2^\top \boldsymbol{\beta} &= \beta_2 - \beta_1 \\
\mathbf{g}_3^\top \boldsymbol{\beta} &= \alpha_2 - \alpha_1
\end{align}
So, we have three linearly independent estimable functions. Now, only $\mathbf{g}_2^\top \boldsymbol{\beta}$ and $\mathbf{g}_3^\top \boldsymbol{\beta}$ can be considered contrasts, since the sum of its coefficients (or, the row sum of the respective vector $\mathbf{g}$) is equal to zero.
Going back to a one-way balanced model
$$y_{ij}=\mu + \alpha_i + \varepsilon_{ij}, \quad i=1,2, \ldots, k \, , j=1,2,\ldots,n.$$
And suppose we want to test the hypothesis $H_0: \alpha_1 = \ldots = \alpha_k$.
In this setting the matrix $\mathbf{X}$ is not full-rank, so $\boldsymbol{\beta}=(\mu,\alpha_1,\ldots,\alpha_k)^\top$ is not unique and not estimable. To make it estimable we can multiply $\boldsymbol{\beta}$ by $\mathbf{g}^\top$, as long as $\sum_{i} g_i = 0$. In other words, $\sum_{i} g_i \alpha_i$ is estimable iff $\sum_{i} g_i = 0$.
Why this is true?
We know that $\mathbf{g}^\top \boldsymbol{\beta}=(0,g_1,\ldots,g_k) \boldsymbol{\beta} = \sum_{i} g_i \alpha_i$ is estimable iff there exists a vector $\mathbf{a}$ such that $\mathbf{g}^\top = \mathbf{a}^\top \mathbf{X}$.
Taking the distinct rows of $\mathbf{X}$ and $\mathbf{a}^\top=[a_1,\ldots,a_k]$, then:
$$[0,g_1,\ldots,g_k]=\mathbf{g}^\top=\mathbf{a}^\top \mathbf{X} = \left(\sum_i a_i,a_1,\ldots,a_k \right)$$
And the result follows.
If we would like to test a specific contrast, our hypothesis is $H_0: \sum g_i \alpha_i = 0$. For instance: $H_0: 2 \alpha_1 = \alpha_2 + \alpha_3$, which can be written as $H_0: \alpha_1 = \frac{\alpha_2+\alpha_3}{2}$, so we are comparing $\alpha_1$ to the average of $\alpha_2$ and $\alpha_3$.
This hypothesis can be expressed as $H_0: \mathbf{g}^\top \boldsymbol{\beta}=0$, where ${\mathbf{g}}^\top = (0,g_1,g_2,\ldots,g_k)$. In this case, $q=1$ and we test this hypothesis with the following statistic:
$$F=\cfrac{\left[\mathbf{g}^\top \hat{\boldsymbol{\beta}}\right]^\top \left[\mathbf{g}^\top(\mathbf{X}^\top\mathbf{X})^{-}\mathbf{g} \right]^{-1}\mathbf{g}^\top \hat{\boldsymbol{\beta}}}{SSE/k(n-1)}.$$
If $H_0: \alpha_1 = \alpha_2 = \ldots = \alpha_k$ is expressed as $\mathbf{G}\boldsymbol{\beta}=\boldsymbol{0}$ where the rows of the matrix
$$\mathbf{G} = \begin{bmatrix} \mathbf{g}_1^\top \\ \mathbf{g}_2^\top \\ \vdots \\ \mathbf{g}_k^\top \end{bmatrix}$$
are mutually orthogonal contrasts (${\mathbf{g}_i^\top\mathbf{g}}_j = 0$), then we can test $H_0: \mathbf{G}\boldsymbol{\beta}=\boldsymbol{0}$ using the statistic $F=\cfrac{\frac{\mbox{SSH}}{\mbox{rank}(\mathbf{G})}}{\frac{\mbox{SSE}}{k(n-1)}}$, where $\mbox{SSH}=\left[\mathbf{G}\hat{\boldsymbol{\beta}}\right]^\top \left[\mathbf{G}(\mathbf{X}^\top\mathbf{X})^{-1} \mathbf{G}^\top \right]^{-1}\mathbf{G}\hat{\boldsymbol{\beta}}$.
Example 3
To understand this better, let's use $k=4$, and suppose we want to test $H_0: \alpha_1 = \alpha_2 = \alpha_3 = \alpha_4,$ which can be expressed as
$$H_0: \begin{bmatrix} \alpha_1 - \alpha_2 \\ \alpha_1 - \alpha_3 \\ \alpha_1 - \alpha_4 \end{bmatrix} =
\begin{bmatrix} 0 \\ 0 \\ 0 \end{bmatrix}$$
Or, as $H_0: \mathbf{G}\boldsymbol{\beta}=\boldsymbol{0}$:
$$H_0:
\underbrace{\begin{bmatrix}
0 & 1 & -1 & \phantom{-}0 & \phantom{-}0 \\
0 & 1 & \phantom{-}0 & -1 & \phantom{-}0 \\
0 & 1 & \phantom{-}0 & \phantom{-}1 & -1
\end{bmatrix}}_{{\mathbf{G}}, \mbox{our contrast matrix}}
\begin{bmatrix}
\mu \\
\alpha_1 \\
\alpha_2 \\
\alpha_3 \\
\alpha_4
\end{bmatrix} =
\begin{bmatrix}
0 \\
0 \\
0
\end{bmatrix}$$
So, we see that the three rows of our contrast matrix are defined by the coefficients of the contrasts of interest. And each column gives the factor level that we are using in our comparison.
Pretty much all I've written was taken\copied (shamelessly) from Rencher & Schaalje, "Linear Models in Statistics", chapters 8 and 13 (examples, wording of theorems, some interpretations), but other things like the term "contrast matrix" (which, indeed, doesn't appear in this book) and its definition given here were my own.
Relating OP's contrast matrix to my answer
One of OP's matrix (which can also be found in this manual) is the following:
> contr.treatment(4)
2 3 4
1 0 0 0
2 1 0 0
3 0 1 0
4 0 0 1
In this case, our factor has 4 levels, and we can write the model as follows:
This can be written in matrix form as:
\begin{align}
\begin{bmatrix}
y_{11} \\
y_{21} \\
y_{31} \\
y_{41}
\end{bmatrix}
=
\begin{bmatrix}
\mu \\
\mu \\
\mu \\
\mu
\end{bmatrix}
+
\begin{bmatrix}
a_1 \\
a_2 \\
a_3 \\
a_4
\end{bmatrix}
+
\begin{bmatrix}
\varepsilon_{11} \\
\varepsilon_{21} \\
\varepsilon_{31} \\
\varepsilon_{41}
\end{bmatrix}
\end{align}
Or
\begin{align}
\begin{bmatrix}
y_{11} \\
y_{21} \\
y_{31} \\
y_{41}
\end{bmatrix}
=
\underbrace{\begin{bmatrix}
1 & 1 & 0 & 0 & 0 \\
1 & 0 & 1 & 0 & 0\\
1 & 0 & 0 & 1 & 0\\
1 & 0 & 0 & 0 & 1\\
\end{bmatrix}}_{\mathbf{X}}
\underbrace{\begin{bmatrix}
\mu \\
a_1 \\
a_2 \\
a_3 \\
a_4
\end{bmatrix}}_{\boldsymbol{\beta}}
+
\begin{bmatrix}
\varepsilon_{11} \\
\varepsilon_{21} \\
\varepsilon_{31} \\
\varepsilon_{41}
\end{bmatrix}
\end{align}
Now, for the dummy coding example on the same manual, they use $a_1$ as the reference group. Thus, we subtract Row 1 from every other row in matrix $\mathbf{X}$, which yields the $\widetilde{\mathbf{X}}$:
\begin{align}
\begin{bmatrix}
1 & \phantom{-}1 & 0 & 0 & 0 \\
0 & -1 & 1 & 0 & 0\\
0 & -1 & 0 & 1 & 0\\
0 & -1 & 0 & 0 & 1
\end{bmatrix}
\end{align}
If you observe the numeration of the rows and columns in the contr.treatment(4) matrix, you'll see that they consider all rows and only the columns related to the factors 2, 3, and 4. If we do the same in the above matrix yields:
\begin{align}
\begin{bmatrix}
0 & 0 & 0 \\
1 & 0 & 0\\
0 & 1 & 0\\
0 & 0 & 1
\end{bmatrix}
\end{align}
This way, the contr.treatment(4) matrix is telling us that they are comparing factors 2, 3 and 4 to factor 1, and comparing factor 1 to the constant (this is my understanding of the above).
And, defining $\mathbf{G}$ (i.e. taking only the rows that sum to 0 in the above matrix):
\begin{align}
\begin{bmatrix}
0 & -1 & 1 & 0 & 0\\
0 & -1 & 0 & 1 & 0\\
0 & -1 & 0 & 0 & 1
\end{bmatrix}
\end{align}
We can test $H_0: \mathbf{G}\boldsymbol{\beta}=0$ and find the estimates of the contrasts.
hsb2 = read.table(
'https://stats.idre.ucla.edu/stat/data/hsb2.csv',
header=T, sep=",")
y <- hsb2$write
dummies <- model.matrix(~factor(hsb2$race) + 0)
X <- cbind(1,dummies)
# Defining G, what I call contrast matrix
G <- matrix(0,3,5)
G[1,] <- c(0,-1,1,0,0)
G[2,] <- c(0,-1,0,1,0)
G[3,] <- c(0,-1,0,0,1)
G
[,1] [,2] [,3] [,4] [,5]
[1,] 0 -1 1 0 0
[2,] 0 -1 0 1 0
[3,] 0 -1 0 0 1
# Estimating Beta
X.X<-t(X)%*%X
X.y<-t(X)%*%y
library(MASS)
Betas<-ginv(X.X)%*%X.y
# Final estimators:
G%*%Betas
[,1]
[1,] 11.541667
[2,] 1.741667
[3,] 7.596839
And the estimates are the same.
Relating @ttnphns' answer to mine.
On their first example, the setup has a categorical factor A having three levels. We can write this as the model (suppose, for simplicity, that $j=1$):
$$y_{ij}=\mu+a_i+\varepsilon_{ij}\, , \quad \mbox{for } i=1,2,3$$
And suppose we want to test $H_0: a_1 = a_2 = a_3$, or $H_0: a_1 - a_3 = a_2 - a_3=0$, with $a_3$ as our reference group/factor.
This can be written in matrix form as:
\begin{align}
\begin{bmatrix}
y_{11} \\
y_{21} \\
y_{31}
\end{bmatrix}
=
\begin{bmatrix}
\mu \\
\mu \\
\mu
\end{bmatrix}
+
\begin{bmatrix}
a_1 \\
a_2 \\
a_3
\end{bmatrix}
+
\begin{bmatrix}
\varepsilon_{11} \\
\varepsilon_{21} \\
\varepsilon_{31}
\end{bmatrix}
\end{align}
Or
\begin{align}
\begin{bmatrix}
y_{11} \\
y_{21} \\
y_{31}
\end{bmatrix}
=
\underbrace{\begin{bmatrix}
1 & 1 & 0 & 0 \\
1 & 0 & 1 & 0 \\
1 & 0 & 0 & 1 \\
\end{bmatrix}}_{\mathbf{X}}
\underbrace{\begin{bmatrix}
\mu \\
a_1 \\
a_2 \\
a_3
\end{bmatrix}}_{\boldsymbol{\beta}}
+
\begin{bmatrix}
\varepsilon_{11} \\
\varepsilon_{21} \\
\varepsilon_{31}
\end{bmatrix}
\end{align}
Now, if we subtract Row 3 from Row 1 and Row 2, we have that $\mathbf{X}$ becomes (I will call it $\widetilde{\mathbf{X}}$:
\begin{align}
\widetilde{\mathbf{X}} =\begin{bmatrix}
0 & 1 & 0 & -1 \\
0 & 0 & 1 & -1 \\
1 & 0 & 0 & \phantom{-}1 \\
\end{bmatrix}
\end{align}
Compare the last 3 columns of the above matrix with @ttnphns' matrix $\mathbf{L}$. Despite of the order, they are quite similar.
Indeed, if multiply $\widetilde{\mathbf{X}} \boldsymbol{\beta}$, we get:
\begin{align}
\begin{bmatrix}
0 & 1 & 0 & -1 \\
0 & 0 & 1 & -1 \\
1 & 0 & 0 & \phantom{-}1 \\
\end{bmatrix}
\begin{bmatrix}
\mu \\
a_1 \\
a_2 \\
a_3
\end{bmatrix}
=
\begin{bmatrix}
a_1 - a_3 \\
a_2 - a_3 \\
\mu + a_3
\end{bmatrix}
\end{align}
So, we have the estimable functions: $\mathbf{c}_1^\top \boldsymbol{\beta} = a_1-a_3$; $\mathbf{c}_2^\top \boldsymbol{\beta} = a_2-a_3$; $\mathbf{c}_3^\top \boldsymbol{\beta} = \mu + a_3$.
Since $H_0: \mathbf{c}_i^\top \boldsymbol{\beta} = 0$, we see from the above that we are comparing our constant to the coefficient for the reference group (a_3); the coefficient of group1 to the coefficient of group3; and the coefficient of group2 to the group3. Or, as @ttnphns said:
"We immediately see, following the coefficients, that the estimated Constant will equal the Y mean in the reference group; that parameter b1 (i.e. of dummy variable A1) will equal the difference: Y mean in group1 minus Y mean in group3; and parameter b2 is the difference: mean in group2 minus mean in group3."
Moreover, observe that (following the definition of contrast: estimable function+row sum =0), that the vectors $\mathbf{c}_1$ and $\mathbf{c}_2$ are contrasts. And, if we create a matrix $\mathbf{G}$ of constrasts, we have:
\begin{align}
\mathbf{G} =
\begin{bmatrix}
0 & 1 & 0 & -1 \\
0 & 0 & 1 & -1
\end{bmatrix}
\end{align}
Our contrast matrix to test $H_0: \mathbf{G}\boldsymbol{\beta}=0$
Example
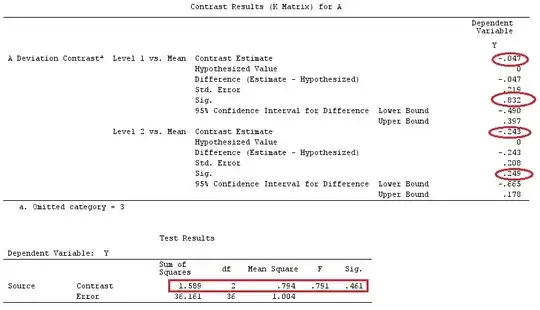
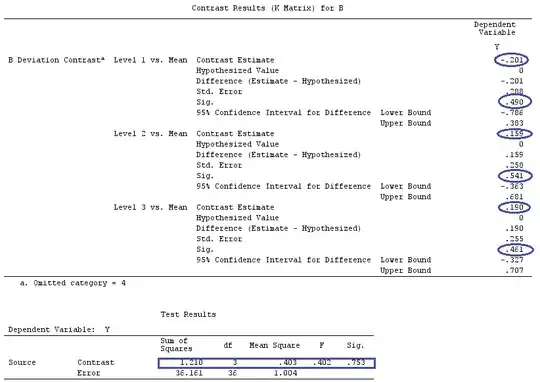
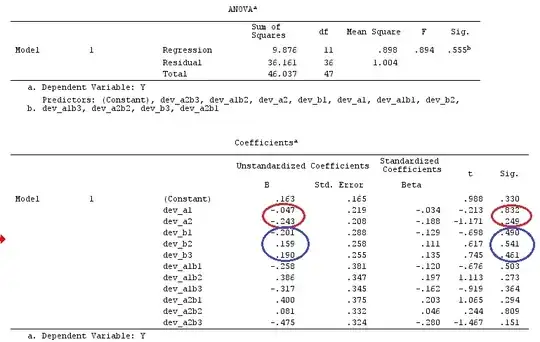
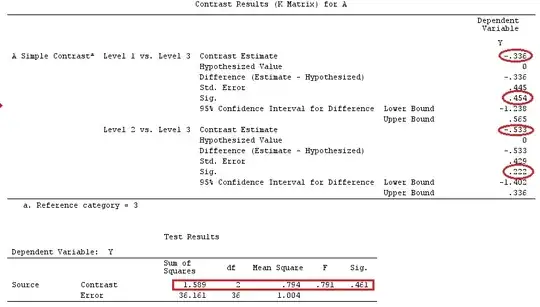
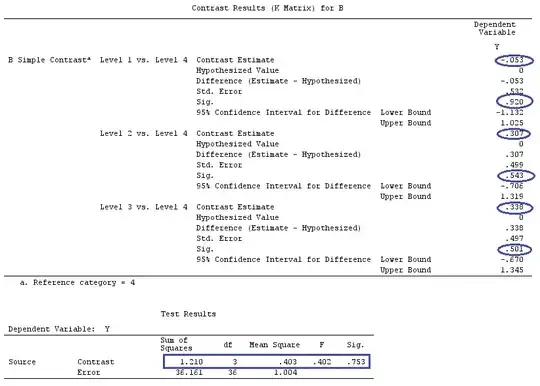
We will use the same data as @ttnphns' "User defined contrast example" (I'd like to mention that the theory that I've written here requires a few modifications to consider models with interactions, that's why I chose this example. However, the definitions of contrasts and - what I call - contrast matrix remain the same).
Y <- c(0.226, 0.6836, -1.772, -0.5085, 1.1836, 0.5633,
0.8709, 0.2858, 0.4057, -1.156, 1.5199, -0.1388,
0.4865, -0.7653, 0.3418, -1.273, 1.4042, -0.1622,
0.3347, -0.4576, 0.7585, 0.4084, 1.4165, -0.5138,
0.9725, 0.2373, -1.562, 1.3985, 0.0397, -0.4689,
-1.499, -0.7654, 0.1442, -1.404,-0.2201, -1.166,
0.7282, 0.9524, -1.462, -0.3478, 0.5679, 0.5608,
1.0338, -1.161, -0.1037, 2.047, 2.3613, 0.1222)
F_ <- c(1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 2, 2, 3, 3,
3, 3, 3, 3, 3, 3, 3, 3, 3, 4, 4, 4, 4, 4, 4, 4, 4, 4, 5,
5, 5, 5, 5, 5, 5, 5, 5, 5, 5)
dummies.F <- model.matrix(~as.factor(F_)+0)
X_F<-cbind(1,dummies.F)
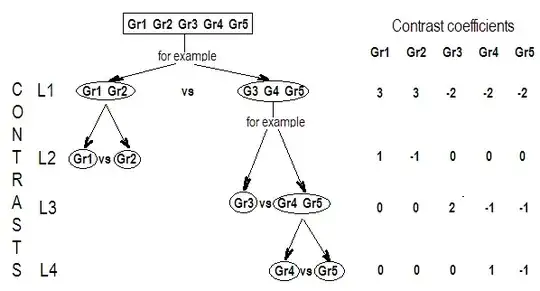
G_F<-matrix(0,4,6)
G_F[1,]<-c(0,3,3,-2,-2,-2)
G_F[2,]<-c(0,1,-1,0,0,0)
G_F[3,]<-c(0,0,0,2,-1,-1)
G_F[4,]<-c(0,0,0,0,1,-1)
G
[,1] [,2] [,3] [,4] [,5] [,6]
[1,] 0 3 3 -2 -2 -2
[2,] 0 1 -1 0 0 0
[3,] 0 0 0 2 -1 -1
[4,] 0 0 0 0 1 -1
# Estimating Beta
X_F.X_F<-t(X_F)%*%X_F
X_F.Y<-t(X_F)%*%Y
Betas_F<-ginv(X_F.X_F)%*%X_F.Y
# Final estimators:
G_F%*%Betas_F
[,1]
[1,] 0.5888183
[2,] -0.1468029
[3,] 0.6115212
[4,] -0.9279030
So, we have the same results.
Conclusion
It seems to me that there isn't one defining concept of what a contrast matrix is.
If you take the definition of contrast, given by Scheffe ("The Analysis of Variance", page 66), you'll see that it's an estimable function whose coefficients sum to zero. So, if we wish to test different linear combinations of the coefficients of our categorical variables, we use the matrix $\mathbf{G}$. This is a matrix in which the rows sum to zero, that we use to multiply our matrix of coefficients by in order to make those coefficients estimable. Its rows indicate the different linear combinations of contrasts that we are testing and its columns indicate which factors (coefficients) are being compared.
As the matrix $\mathbf{G}$ above is constructed in a way that each of its rows is composed by a contrast vector (which sum to 0), for me it makes sense to call $\mathbf{G}$ a "contrast matrix" (Monahan - "A primer on linear models" - also uses this terminology).
However, as beautifully explained by @ttnphns, softwares are calling something else as "contrast matrix", and I couldn't find a direct relationship between the matrix $\mathbf{G}$ and the built-in commands/matrices from SPSS (@ttnphns) or R (OP's question), only similarities. But I believe that the nice discussion/collaboration presented here will help clarify such concepts and definitions.