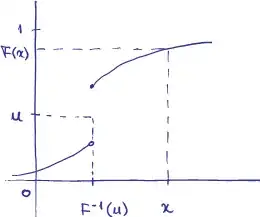
For a CDF that is not strictly increasing, i.e. its inverse is not defined, define the quantile function
$$F^{-1} (u) =\inf \{x: F(x) \geq u \},\quad 0<u<1. $$
Where U has a uniform $(0,1)$ distribution. Prove that the random variable $F^{-1} (u)$ has cdf $F(x)$.
In case of a strictly increasing CDF the proof is quite easy because the inverse is defined. Define $X=F^{-1} (u)$
$$ P\left[X<x \right]= P \left [F^{-1} (U) \leq x \right]= P \left[U \leq F(x) \right] =F(x) $$
But how do I accomondate the nondecreasing CDF whose inverse is given by the quantile function? I am a begginer so any help is welcome. Thank you.