I am trying to figure out if this Markov chain is irreducible and if it is aperiodic and why or why not.
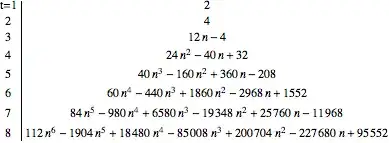
For me it is not irreducible Markov chain because you cannot go from state 2, 5 or 6 to any of the states 1, 3, 4. I don't know if my argument is good.
