Is the absolute value of the difference between two Poisson distributions a Poisson distribution?

Question

What is the distribution of the absolute value of the Skellam distribution?

Answer 1

Two quite different questions!

Is the absolute value of the difference between two Poisson distributions a Poisson distribution?

This one is easily answered: clearly no, since the relationship between the mean and variance doesn't hold.

what is the distribution of the absolute value of the Skellam distribution.

This second one is a little trickier. I'm working on a nicer way to do that than the brute force of stupidity direct methods. But since I don't seem to be clever today, here's one of the brute force of stupidity direct methods:

Let $Z = \max(X,Y) - \min(X,Y)$

\begin{eqnarray} P(Z=0) &=& \sum_{i=0}^\infty P(X=i)P(Y=i) \\ &=& \sum_{i=0}^\infty [\exp(-\mu_1)\mu_1^i/i! \exp(-\mu_2)\mu_2^i/i!\\ &=& \sum_{i=0}^\infty [\exp(-(\mu_1+\mu_2))(\mu_1\mu_2)^i/(i!)^2\\ &=& \exp(-(\mu_1+\mu_2)) \sum_{i=0}^\infty (\mu_1\mu_2)^i/(i!)^2\\ &=& \exp(-(\mu_1+\mu_2)) \sum_{i=0}^\infty g^{2i}/(i!)^2\\ &=& \exp(-(\mu_1+\mu_2)) \sum_{i=0}^\infty (2g/2)^{2i}/(i!)^2 \end{eqnarray}

where $g =\sqrt{\mu_1\mu_2}$

Now $I_\alpha(x) =\sum_{m=0}^\infty \frac{1}{m! \Gamma(m+\alpha+1)}\left(\frac{x}{2}\right)^{2m+\alpha}$, where $I_\alpha(x)$ is a modified Bessel function of the first kind.

so

$$P(Z=0) = \exp(-(\mu_1+\mu_2)) I_0(2g)$$.

Now, for $j = 1,2,...$,

\begin{eqnarray} P(Z=j) &=& \sum_{i=0}^\infty [P(X=i)P(Y=i+j) + P(X=i+j)P(Y=i)] \\ &=& \sum_{i=0}^\infty [\exp(-\mu_1)\mu_1^i/i!\exp(-\mu_2)\mu_2^{i+j}/(i+j)!\\ & & \quad\quad + \exp(-\mu_2)\mu_2^i/i! \exp(-\mu_1)\mu_1^{i+j}/(i+j)!]\\ &=& \exp(-(\mu_1+\mu_2))\sum_{i=0}^\infty [g^{2i}(\mu_2^j + \mu_1^j)]/[i!(i+j)]!\\ &=& \exp(-(\mu_1+\mu_2))(\mu_2^j + \mu_1^j)\sum_{i=0}^\infty g^{2i}/[i!(i+j)]!\\ &=& \exp(-(\mu_1+\mu_2))(\mu_2^j + \mu_1^j)/g^j\sum_{i=0}^\infty g^{2i+j}/[i!(i+j)]!\\ &=& \exp(-(\mu_1+\mu_2))(\mu_2^j + \mu_1^j)/g^j\sum_{i=0}^\infty (2g/2)^{2i+j}/[i!(i+j)]!\\ &=& \exp(-(\mu_1+\mu_2))(\mu_2^j + \mu_1^j)/g^j I_j(2g) \end{eqnarray}

...assuming I didn't make errors - which I easily could have.

Another direct alternative would be to try to work with the Skellam distribution itself, but I don't think it's going to be any nicer.

---

Now, how do we check I didn't make a mistake?

I see a couple of approaches:

One check is to see if for some examples, the values sum to 1.

Another way is to compute a few values by direct summation, truncated when the terms become very small (the probabilities decrease quite rapidly) and compare with the above results.

Yet another is simulation.

(i) First, a function to compute the pmf:

 dabskel <- function(x,mu1,mu2) {
   g <- sqrt(mu1*mu2)
   emm <- exp(-(mu1+mu2))
   emm*besselI(2*g,x)*ifelse(x==0,1,(mu2^x + mu1^x)/g^x)
 }

> sum(dabskel(0:20,1,1))  # 20 should be plenty far enough to make it sum to 1
[1] 1
> sum(dabskel(0:20,3,2))
[1] 1

So it seems to sum to 1. Good start

(ii) Now compute directly:

x <- 0:8
y <- x
f <- function(x,y)dpois(x,3)*dpois(y,2)
probs <- outer(x,y,f)
f2 <- function(x,y)pmax(x,y)-pmin(x,y)
vals <- outer(x,y,f2)
asmres <- tapply(c(probs),c(vals),FUN=sum,simplify=TRUE)

(iii) Now simulate

 xyar=abs(rpois(100000,3)-rpois(100000,2))

And compare them:

plot(x,dabskel(x,3,2),type="h")
points(x+.04,asmres,col=2,type="h")
points(x+.08,table(xyar)[1:9]/100000,col=4,type="h")

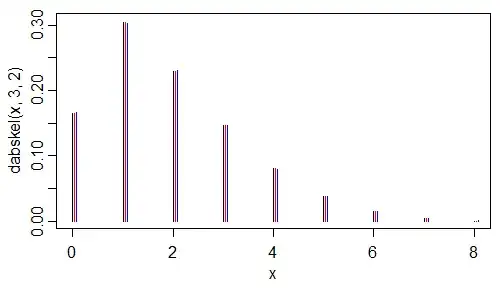
Black is the function worked out above, red is the direct-but-truncated calculation and the blue is the simulated distribution. Looks like it's okay.

Answer 2

OP: what is the distribution of the absolute value of the Skellam distribution

Let $X$ ~ SkellamDistribution$(a,b)$, with pmf $f(x)$:

$$f(x) = e^{-a-b} \left(\frac{a}{b}\right)^{x/2} I_x\left(2 \sqrt{a b}\right)$$

Then, the pmf of $Y=|X|$ will be, say $g(y)$:

$$g(y) = \begin{cases}f(0) & y = 0 \\ f(y) + f(-y) & y \ge 1 \end{cases}$$

All done.