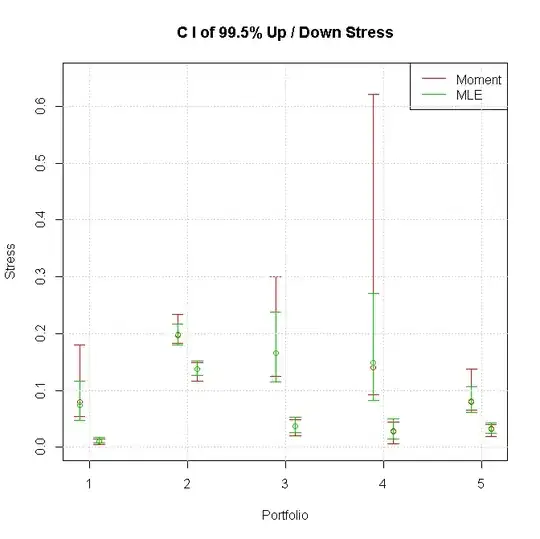
I have got some small data sets (about 8 to 11 data points for each set), following Normal distribution. I would like to find out the 95% confidence interval of the 0.005 and 0.995 percentile of each set.
Firstly, moment estimation method is employed to estimate the Normal distribution parameters, and their confidence interval is built by (mu~Normal, sigma^2~Chi-square) theorem. And find the CI of percentile by simulation.
Secondly, MLE method is also employed and the parameter's CI is built by MLE~asymptotic Normal theorem. Then find the CI of percentile by simulation.
As the figure shows, the MLE CI is much narrow than Moment method. We know that MLE is efficient, leading small variance and narrow CI. This understanding is consistent with our figure.
But my MLE CI approach is based on asymptotic assumption, while my amount of data points is quite small. Would this (too small data amount) leads MLE's CI incorrect and worse than moment method? or it is still more efficient than moment method?
Is the MLE CI too narrow to contain the 95% probability of the true value, if the amount is too small?