2

I am trying to estimate the precision $\tau$ of a normal distribution with either WinBUGS or OpenBUGS:

$c \sim \text{normal}(\mu,\tau)$

$\mu \rightarrow \lambda \cdot t^{-\beta}$

$\tau \sim \text{gamma}(0.1,0.001)$

I tried using a standard approach here by setting $\tau\sim \text{gamma}(0.001,0.001)$ but WinBUGS and OpenBUGS both stop with an error message. WinBUGS basically tells me to increase the parameters for the gamma prior.

However, if I do that, the MCMC chains of $\tau$ act strangely, even if I run 200.000 iterations with thin=200:

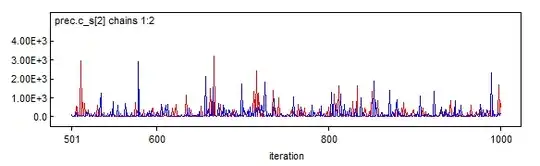
precision MCMC

As you can see, the chains have spikes of up to 3000and in other cases even more. I'm not very experienced but I think this shouldn't be the case. The parameter $c$ is in the range of [0;1] so I'm worried about precision estimates of above 400.

This question seems to address my issue. It says that Gibbs samplers (like WinBUGS) have problems estimating the precision of a normal if the parameters of the gamma distribution are close to zero (which is not exactly true for my case, but they are fairly small). Playing around with the parameters of the gamma distribution does help but I thought the whole purpose of using a gamma prior is to approximate a uniform which is close to zero.

I have also tried estimating the precision indirectly by estimating the standard deviation as a uniform distribution first but the result was more or less the same.

Any help is highly appreciated.

Community
  • 1
Gerome Bochmann
  • 227
  • 3
  • 11
  • Some quick comments: it would be helpful to know how much data you put into it and what type of model you are fittig (i.e. what role do lambda, t, and beta play? is this some sort of decay model?). Otherwise remember that if your posterior sd is close to zero your precision will automatically vary a lot. Actually look at the sd might be rather comforting. For example, having an sd that varies between 0.1 and 0.01 means that the precision will vary between 100 and 1000. – Erik Nov 13 '13 at 15:43
  • Yes, this is a power function fit of memory decay. I'm not sure what you mean by how much data but there are nine time (t) intervalls at which participants respond. For each t there are approximately 300 responses. The original paper didn't report any sd for c. If I directly estimate the sd it varies between 0 and 10 so this seems to be okay, then. – Gerome Bochmann Nov 13 '13 at 15:57
  • Independently of your question, using a gamma distribution for $\tau$ is a bit depreceated (see e.g. http://stats.stackexchange.com/questions/6493/weakly-informative-prior-distributions-for-scale-parameters/28420#28420). Moreover in your case, I guess that you could use the Jeffreys prior for $\tau$. – peuhp Nov 14 '13 at 08:09
  • Since, I'm using BUGS, this should pose a problem. As far as I understand, the Jeffreys prior is improper and Bugs usually requires proper priors. – Gerome Bochmann Nov 14 '13 at 16:43
  • 1
    @peuhp the resource you link is studying priors for *variance*, not precision ($\tau$). $\tau = 1/var$. Using `dgamma` prior for $\tau$ is [perfectly OK](http://www.unc.edu/courses/2010fall/ecol/563/001/docs/lectures/lecture14.htm#precision) and will hardly become obsolete :) – Tomas Nov 26 '13 at 23:23
  • @Tomas. I am not so sure, the gamma prior for precision consists in the conjugate-choice and to my knownledge has no serious uninformative property (just as the inverse-gamma for variance). By contrast, half-cauchy or beta-2 prior seems to offer more interesting properties. Moreover, I already used he improper Jeffreys into Jags (maybe I was wrong), so I guess the same can be said about BUGS. Maybe I miss some points about dgamma for precision. Please, let me know if it is the case. – peuhp Nov 27 '13 at 08:12
  • @peuhp I don't know, I use the recommendation using the resource I cited - and it was actually recommended by many others. I know, this doesn't mean that its perfect. Unfortunatelly the source you cite mentions the priors for *var* not *precision* so it does not exactly compare those to `dgamma`, or does it? Or, is there any resource that states that `dgamma` is worse than something else? – Tomas Nov 27 '13 at 12:20
  • @Tomas. I may be wrong but as I understand it, both formulations are equivalent as if $ X \sim \mbox{Gamma}(k, \theta)$ then $\frac{1}{X} \sim \mbox{Inv-Gamma}(k, \theta^{-1})$ ... So recommendations (here warnings) for the inverse gamma to $\sigma^2$ applied for the gamma to $\tau$. If it is correct there are many resources stating that dgmma is worse than something else (e.g. http://www.ime.unicamp.br/~veronica/ME705/T2.pdf). – peuhp Nov 28 '13 at 08:04

1 Answers1

2

I had exactly the same with specifying dgamma(0.001, 0.001) for WinBUGS! Jags can actually take it (and I recommend you to use Jags if you don't need advanced WinBUGS features; and even if you want to use WinBUGS, it comes in handy for debugging, because Jags has much more comprehensible error reporting), but for WinBUGS, you must do:

 x[..] ~ dnorm(mean[..], tau)

 tau ~ dgamma(0.01, 0.01)

Don't be afraid, dgamma is a good choice. You just have to tweak the parameters. Follow this resource which perfectly explains gamma parameters and prior choice! http://www.unc.edu/courses/2010fall/ecol/563/001/docs/lectures/lecture14.htm#precision

Also note that it might come in handy to normalize the input variables - it makes parameter estimation (and prior choice) much more smooth and easier, because the basic priors will work perfectly with the usual constants.

Tomas
  • 5,735
  • 11
  • 52
  • 93
  • What exactly do you mena by normalize? – Gerome Bochmann Mar 20 '14 at 13:07
  • I mean, I have an idea what this means in general but "normalizing the input variables" is a new concept for me. – Gerome Bochmann Mar 20 '14 at 14:20
  • Also, I have tried using JAGS and it also runs into numerical problems with this prior. I'm estimating quite a few parameters. Basically, I'm estimating task performance at different intervals in the first step. In the second step, I'm using these parameters to do non-linear regression. – Gerome Bochmann Mar 20 '14 at 14:25