Why is this happening with the $\chi^2$ test? Is there a test without this sample size problem?

Question

I haven't found a satisfactory answer for this problem by reading previous related posts. There are a total of $10,000,000$ observations with the following observed and expected frequencies:

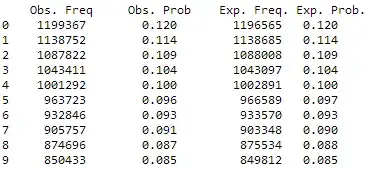
A goodness-of-fit $\chi^2$-test comparing the observed data to the expected probabilities yields a value of $25.97749$ with $p$-value $.002$. This result seems--at least to the non-expert--quite shocking given how similar the observed distribution is to the expected distribution.

If I draw less observations (in fact, Obs. Freq come from simulations), say $1000$, then the $\chi^2$-test gives a $p$-value close to 1.

1) Is there a formal way to know when are we using too much observations?

2) Is there a goodness-of-fit test that can handle $10,000,000$ observations?

Any help is appreciated.

EDIT: Just some background of the data and the purpose of the test. The simulations come from multiplying normal and exponential distributions; the observed frequencies reported are those of the 2nd significant digits of these simulations. The expected frequencies come from what Benford's law for the 2nd significant digit predicts.

So the table show that the simulated variables follow closely what is predicted by Benford's law. The reason why the table is not enough is that we would like to automatize the analysis for several datasets and detect whenever a deviation occurs.

Answer 1

1. Unless your observations have a cost-benefit tradeoff of some kind (e.g. paying subjects) then there's not really any such thing as too many. More observations give better parameter estimates.
2. The test you used handled 10,000,000 observations just fine.

Your "problem" isn't a problem at all. The estimate of a parameter becomes very good when N is very large to the point that any measurable deviation from no difference becomes a statistically significant difference. That doesn't mean the difference is meaningful or practically significant. That's a judgment call you'll have to make.

One way to help you is to calculate an effect size. Typically Cramér's V ($\phi_c$) is used. Note that for goodness of fit you use the rows instead of smallest dimension and it is interpreted as the tendency toward a singular outcome. Cramér's V for your experiment is going to be an extraordinarily tiny number, suggesting the effect is very small.

But in this case, the numbers so obviously tell a tale of a very small effect I think that just showing the numbers is sufficient. What you would say is that the expected probabilities are nearly identical to the observed and leave it at that.

You might find this question and the answers helpful.

EDIT: OK, so the values are of simulations. I'm guessing they're simulations where the null is true. If that's the case then the significant effect is a Type I error. My guess is that you're not running lots of simulations. You need to do that in order to see how the distribution of p-values works. You don't just run one simulation and remain puzzled. It's a simple calculation. Do it again, and again. In fact, write one that will generate lots of p-values for you. What you'll find is that it is equally, absolutely equally, as easy to get a high p-value or low p-value with 10,000,000 as it is with 1000. In R, this simulation would be easy.

ntests <- 1000
N <- 1000 # change this to whatever value you like
p <- c(0.120, 0.114, 0.109, 0.104, 0.1, 0.097, 0.093, 0.090, 0.088, 0.085) 
pVals <- replicate(ntests, {
    y <- table( sample(0:9, N, prob = p, replace = TRUE) )
    chisq.test(y, p = p)$p.value })
hist(pVals, freq = FALSE)
sum( pVals < 0.05 ) / ntests

The mean value of the last calculation (proportion of significant effects) is unaffected by N. But, it's more variable when N is small.