I'll try to make the matter as clear as possible given the circumstances. My boss asked me to look at an old report a former employee wrote around a couple of months ago. Apparently the report contains some very useful information but, unfortunately, no one is able to understand it because it is written in "mathematics".
The main node of the report is a linear regression formula for the predictions of future data for non-linear function. Consider to have the following:
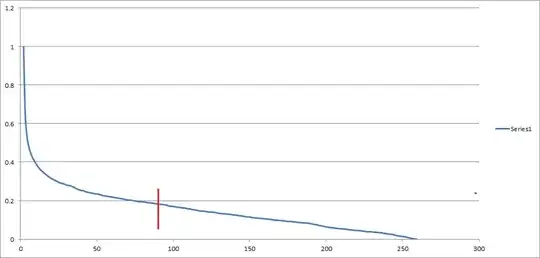
The Y-axis report a percentage (1 equals 100%). Now imagine to only have the part of the data before the red line. My former colleague figured out that the formula to estimate the second part of the data was:
$$R(t) = 1 - d t^{1/\alpha}$$
While I did understand most of the formula I cannot understand what $d$ and $\alpha$ represent. By any chance, are they a common sign for something I am missing?
Please, ask if something is not clear.