I've read that homoskedasticity means that the standard deviation of the error terms are consistent and don't depend on the x-value.
Question 1: Can someone explain intuitively why this is necessary? (An applied example would be great!)
Question 2: I can never remember whether it's hetero- or homo- that is ideal. Can someone explain the logic of which one is ideal?
Question 3: Heteroskedasticity means that x is correlated with the errors. Can someone explain why this is bad?
Homoskedasticity means that the variances of all the observations are identical to one another, heteroskedasticity means they're different. It's possible that the size of the variances displays some trend relative to x, but it's not strictly necessary; as shown in the accompanying diagram, variances that are differently sized in some random way from point to point will qualify just as well.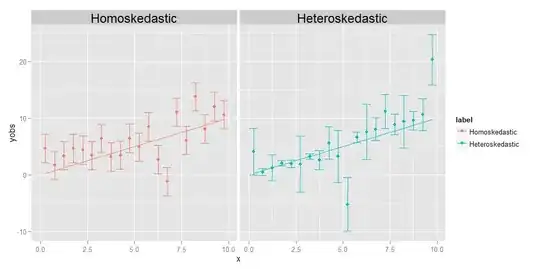
The job of the regression is to estimate an optimal curve which passes as close to as many of the data points as possible. In the case of heteroskedastic data, by definition some points will naturally be much more widely dispersed than others. If the regression simply treats all of the data points equivalently, the ones with the largest variance will tend to have undue influence in selecting the optimal regression curve, by "dragging" the regression curve toward themselves, in order to achieve the objective of minimizing the overall scatter of the data points about the final regression curve.
This issue can easily be overcome by simply weighting each data point in inverse proportion to its variance. This assumes, however, that one knows the variance associated with each individual point. Often, one doesn't. Thus, the reason that homoskedastic data are preferred is because they are simpler and easier to deal with--you can get the "correct" answer for the regression curve without necessarily knowing the underlying variances of the individual points, because the relative weights between the points in some sense will "cancel out" if they are all the same anyway.
EDIT:
A commenter asks me to explain the idea that individual points may have their own, unique, different variances. I do so with a thought experiment. Suppose I ask you to measure the weight vs. length of a bunch of different animals, from the size of a gnat all the way up to the size of an elephant. You do so, plotting length on the x-axis, and weight on the y-axis. But let's pause for a moment to consider things in a little more detail. Let's look at the weight values specifically--how did you actually obtain them? You can't possibly use the same physical measuring device to weigh a gnat as you would to weigh a house pet, nor can you use the same device to weigh a house pet as you would to weigh an elephant. For the gnat, you are probably going to have to use something like an analytical chemistry balance, accurate down to 0.0001 g, while for the house pet, you'd use a bathroom scale, which might be accurate to about a half of a pound or so (roughly around 200 g), while for the elephant, you might use a something like a truck scale, which might only be accurate to within +/- 10 kg. The point is, all of these devices have different inherent accuracies--they only tell you the weight up to a certain number of significant digits, and after that you can't really know for sure. The different sizes of the error bars in the heteroskedastic plot above, which we associate with the different variances of the individual points, reflect differing degrees of certainty about the underlying measurements. In short, different points can have different variances because sometimes we can't measure all of the points equally well--you're never going to know the weight of an elephant down to +/- 0.0001 g, because you can't get that kind of accuracy out of a truck scale. But you can know the weight of a gnat to +/- 0.0001 g, because you can get that kind of an accuracy on an analytical chemistry balance. (Technically, in this particular thought experiment, the same type of issue actually arises for the length measurement as well, but all that really means is that if we decided to plot horizontal error bars representing uncertainties in the x-axis values also, those would have different sizes for different points too.)
Why do we want homoskedasticity in regression?
It's not that we want homoskedasticity or heteroskedasticity in the regression; what we want is for the model to reflect the actual properties of the data. Regression models may be formulated either with an assumption of homoskedasticity, or with an assumption of heteroskedasticity, in some specified form. We want to formulate a regression model that fits with the actual properties of the data, and thus reflects a reasonable specification of the behaviour of data coming from the observed process.
Thus, if the variance of the deviation of the response from its expectation (the error term) is fixed (i.e., is homoskedastic) then we want a model that reflects this. And if the variance of the deviation of the response from its expectation (the error term) depends on the explanatory variable (i.e., is heteroskedastic) then we want a model that reflects this. If we mis-specify the model (e.g., by using a homoskedastic model for heteroskedastic data) then this means that we will mis-specify the variance of the error term. The result is that our estimate of the regression function will under-penalise some errors and over-penalise other errors, and will tend to perform more poorly than if we specify the model correctly.
In addition to the other excellent answers:
Can someone explain intuitively why this is necessary? (An applied example would be great!)
Constant variance isn't necessary, but when it holds modeling and analysis is simpler. Part of this must be historical, analysis when variance is not constant is more complicated, requires more computation! So one developed methods (transformations) to get to a situation where constant variance holds and the simpler/faster methods could be used. Today there are more alternative methods, and fast computation isn't as important as it was. But simplicity is still of value! Part is technical/mathematical. Models with nonconstant variance does not have exact ancillaries (see here.) So only approximate inference is possible. Nonconstant variance in the two-groups problem is the famous Behrens-Fisher problem.
But it is even deeper than that. Let us look at the simplest example, comparing the means of two groups with a (some variant of) t-test. The null hypothesis is that the groups are equal. Say this is a randomized experiment with a treatment and control group. If group sizes are reasonable, randomization should make the groups equal (before treatment.) The constant variance assumption says that the treatment (if it works at all), only influences the mean, not the variance. But how could it influence the variance? If the treatment really works equally on all members of the treatment group, it should have more or less the same effect for all, the group is just shifted. So unequal variance could mean that the treatment has different effect for some members of the treatment group than others. Say, if it has some effect for half the group and a much stronger effect for the other half, the variance will increase together with the mean! So the constant variance assumption is really an assumption about homogeneity of individual treatment effects. When this does not hold one should expect that analysis get more convoluted. See here. Then, with unequal variances, it could also be interesting to ask about reasons for it, specifically if the treatment could have anything to do with it. If so, this post could be of interest.
Question 2: I can never remember whether it's hetero- or homo- that is ideal. Can someone explain the logic of which one is ideal?
No one is ideal, you must model the situation you have! But if this is a question about remembering the meaning of those two funny words, just prepend them to sex and you will remember.
Question 3: Heteroskedasticity means that x is correlated with the errors. Can someone explain why this is bad?
It means that the conditional distribution of the errors given $x$, varies with $x$. That isn't bad, it just makes life complicated. But it might just make life interesting, it might be a signal of something interesting going on.
One of the assumptions of OLS regression is:
Variance of the error term/residual is constant. This assumption is known as homoskedasticity.
This assumption ensures that with the change in observations, the variations in the error term should not change
Also, the estimates of standard error would become biased and unreliable in the presence of heteroskedasticity which leads to a problem in hypothesis testing about estimators.
In summary, in absence of homoskedasticity, we have linear and unbiased estimators but not BLUE (best linear unbiased estimators)
[Read Gauss Markov theorem]
I hope now it’s clear that ideally, we need homoskedasticity in our model.
If the error term is correlated with y or y predicted or any of the xi’s; it indicates that our predictor(s) have not done the job of explaining the variation in ‘y’ correctly.
Somehow, the model specification is not correct or some other issues are there.
Hope it helps! Will try to write an intuitive example soon.
