I think the problem is that you train (or rather: optimize) using your "test" set. In other words, you can do this, but then you need an additional independent test set for the final validation. Or a nested validation set up from the beginning.
This is how I see the problem:
There can be combinations of training and test data (particular splits), where the model trained on that training data works well with the given test set -- regardless of how representative the test set is for the actual problem. Your strategy is actually a search strategy that tries to find such combinations. As there is no guarantee that you'll encounter a really satisfactory model before encountering one of the "fake satisfactory" models, there is trouble lurking.
Because you decide depending on the test set performance whether to go on for a new model or not, your testing is not independent. I think this is related to the problems with other iterative model optimization approaches, where an increase in model quality seems to occur also between equivalent models.
Here's a simulation:
- multivariate normally distributed data, sd = 1 for 25 variates, first 4 informative being 0 for one class and 1 for the other.
- 500 cases of each class in the data set, split 80:20 randomly without replacement into train and "test" sets.
- 50000 cases each class independent test set.
- repeat until "acceptable" accuracy of 90% is reached according to internal test set.
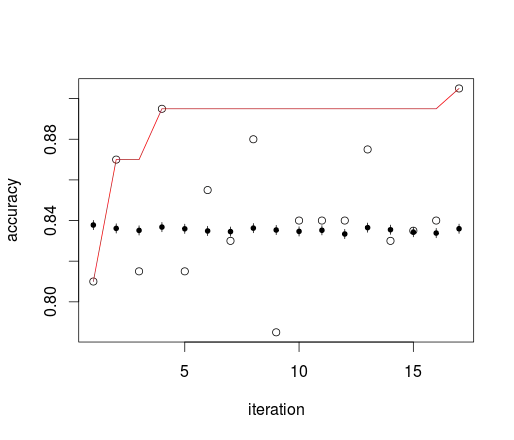
circles: internal test estimate, dots and whiskers: external independent test set with 95% ci (Agresti-Coull method), red line: cumulative maximum of internal estimate.
Your rule basically uses the cumulative maximum of the internal test set. In the example that means that within few iterations, you end up with an optimistic bias that claims 1/3 less errors than your models actually have. Note that the models here cannot be distinguished with a 200 cases test set. The order of differences between the large external test set results is the same as the confidence interval width.
You can also nicely see what I mean with skimming variance: the internal test set estimate itself is unbiased. What causes the bias is doing (potentially large) numbers of iterations and picking the maximum.
Besides the optimization that is hidden in this procedure as well, the problem is of course the large variance of the accuracy. Other performance measures like Brier's score have lower variance and thus do not lead to such serious overfitting that fast.
The code of the simulation:
require ("binom")
require ("MASS")
set.seed (seed=1111)
randomdata <- function (class, n, p = 25, inf = 1:4){
x <- matrix (rnorm (n * p), nrow = n)
x [, inf] <- x [, inf] + class
data.frame (class = class, X = I (x))
}
data <- rbind (randomdata (class = 0, n = 500),
randomdata (class = 1, n = 500))
indeptest <- rbind (randomdata (class = 0, n = 5e4),
randomdata (class = 1, n = 5e4))
internal.acc <- rep (NA, 100)
external.acc <- rep (NA, 100)
for (i in 1 : 100){
i.train <- sample (nrow (data), size=nrow (data) *.8, replace=FALSE)
train <- data [ i.train, ]
test <- data [- i.train,]
model <- lda (class ~ X, train)
pred <- predict (model, test)
indep.pred <- predict (model, indeptest)
#table (reference = test$class, prediction = pred$class)
internal.acc [i] <- sum (diag (table (reference = test$class, prediction = pred$class))) / nrow (test)
external.acc [i] <- sum (diag (table (reference = indeptest$class, prediction = indep.pred$class))) / nrow (indeptest)
if (internal.acc [i] >= 0.9) break ;
cat (".")
}
internal.acc <- internal.acc [1 : i]
external.acc <- external.acc [1 : i]
plot (internal.acc, ylab = "accuracy", xlab = "iteration")
points (external.acc, pch = 20)
lines (cummax (internal.acc), col = "red")
ci <- binom.agresti.coull (external.acc*nrow (indeptest), nrow (indeptest))
segments (x0 = seq_along (external.acc), x1 = seq_along (external.acc), y0 = ci$lower, y1 = ci$upper)
