In To P or not to P: on the evidential nature of P-values and their place in scientic inference, Michael Lew has shown that, at least for the t-test, the one-sided p-value and sample size can be interpreted as an "address" (my term) for a given likelihood function. I have repeated some of his figures below with slight modification. The left column shows the distribution of p-values expected due to theory for different effect sizes (difference between means/pooled sd) and sample sizes. The horizontal lines mark the "slices" from which we get the likelihood functions shown by the right panels for p=0.50 and p=0.025.
These results are consistent with monte carlo simulations. For this figure I compared two groups with n=10 via t-test at a number of different effect sizes and binned 10,000 p-values into .01 intervals for each effect size. Specifically there was one group with mean=0, sd=1 and a second with a mean that I varied from -4 to 4, also with sd=1.
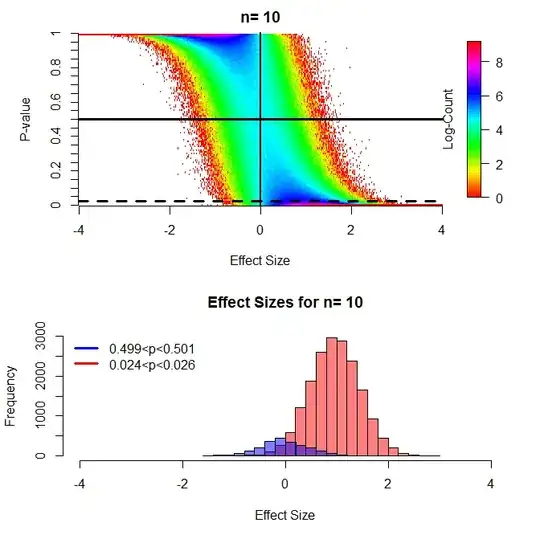
(The above figures can be directly compared to figures 7/8 from the paper linked above and are very similar, I found the heatmaps more informative than the "clouds" used in that paper and also wished to independently replicate his result.)
If we examine the likelihood functions "indexed" by the p-values, the behaviour of rejecting/accepting hypotheses or ignoring results giving p-values greater than 0.05 based on a cut-off value (either the arbitrary 0.05 used everywhere or determined by cost-benefit) appears to be absurd. Why should I not conclude from the n=100, p=0.5 case that "the current evidence shows that any effect, if present, is small"? Current practice would be to either "accept" there is no effect (hypothesis testing) or say "more data needed" (significance testing). I fail to see why I should do either of those things.
Perhaps when a theory predicted a precise point value, then rejecting a hypothesis could make sense. But when the hypotheses are of the form either "mean1=mean2 or mean1!=mean2" I see no value. Under the conditions these tests are often being used randomization does not guarantee all confounds are balanced across groups and there should always be the worry of lurking variables, so rejecting the hypothesis that mean1 exactly equals mean2 has no scientific value as far as I can tell.
Are there cases beyond the t-test where this argument would not apply? Am I missing something of value that rejecting a hypothesis with low a priori probability provides to researchers? Ignoring results above an arbitrary cutoff seems to have lead to widespread publication bias. What useful role does ignoring results play for scientists?
Michael Lew's R code to calculate the p-value distributions
LikeFromStudentsTP<-function(n,x,Pobs,test.type, alt='one.sided'){
# test.type can be 'one.sample', 'two.sample' or 'paired'
# n is the sample size (per group for test.type = 'two.sample')
# Pobs is the observed P-value
# h is a small number used in the trivial differentiation
h<-10^-7
PowerDn<-power.t.test('n'=n, 'delta'=x, 'sd'=1,
'sig.level' = Pobs-h, 'type'= test.type, 'alternative'=alt)
PowerUp<-power.t.test('n'=n, 'delta'=deltaOnSigma, 'sd'=1,
'sig.level' = Pobs+h, 'type'= test.type, 'alternative'=alt)
PowerSlope<-(PowerUp$power-PowerDn$power)/(h*2)
L<-PowerSlope
}
R code for figure 1
deltaOnSigma <- 0.01*c(-400:400)
type<-'two.sample'
alt='one.sided'
p.vals<-seq(0.001,.999,by=.001)
#dev.new()
par(mfrow=c(4,2))
for(n in c(3,5,10,100)){
m<-matrix(nrow=length(deltaOnSigma), ncol=length(p.vals))
cnt<-1
for(P in p.vals){
m[,cnt]<-LikeFromStudentsTP(n,deltaOnSigma,P,type, alt)
cnt<-cnt+1
}
#remove very small values
m[which(m/max(m,na.rm=T)<10^-5)]<-NA
m2<-log(m)
par(mar=c(4.1,5.1,2.1,2.1))
image.plot(m2, axes=F,
breaks=seq(min(m2, na.rm=T),max(m2, na.rm=T),length=1000), col=rainbow(999),
xlab="Effect Size", ylab="P-value"
)
title(main=paste("n=",n))
axis(side=1, at=seq(0,1,by=.25), labels=seq(-4,4,by=2))
axis(side=2, at=seq(0,1,by=.05), labels=seq(0,1,by=.05))
axis(side=4, at =.5, labels="Log-Likelihood", pos=.95, tick=F)
abline(v=0.5, lwd=1)
abline(h=.5, lwd=3, lty=1)
abline(h=.025, lwd=3, lty=2)
par(mar=c(5.1,4.1,4.1,2.1))
plot(deltaOnSigma,m[,which(p.vals==.025)], type="l", lwd=3, lty=2,
xlab="Effect Size", ylab="Likelihood", xlim=c(-4,4),
main=paste("Likelihood functions for","n=",n)
)
lines(deltaOnSigma,m[,which(p.vals==.5)], lwd=3, lty=1)
legend("topleft", legend=c("p=.5","p=.025"), lty=c(1,2),lwd=1, bty="n")
}
R code for figure 2
p.vals<-seq(0,1,by=.01)
deltaOnSigma <- 0.01*c(-400:400)
n<-10
n2<-10
sd2<-1
num.sims<-10000
sp<-sqrt((9*1^2 +(n2-1)*sd2^2)/(n+n2-2))
p.out=matrix(nrow=num.sims*length(deltaOnSigma) ,ncol=2)
m<-matrix(0,nrow=length(deltaOnSigma),ncol=length(p.vals))
pb<-txtProgressBar(min = 0, max = length(deltaOnSigma) ,style = 3)
cnt<-1
cnt2<-1
for(i in deltaOnSigma ){
for(j in 1:num.sims){
m2<-i
a<-rnorm(n,0,1)
b<-rnorm(n,m2,sd2)
p<-t.test(a,b, alternative="less")$p.value
r<-end(which(deltaOnSigma<=m2/sp))[1]
m[r,end(which(p.vals<p))[1]]<-m[r,end(which(p.vals<p))[1]]+1
p.out[cnt,]<-cbind(m2/sp,p)
cnt<-cnt+1
}
cnt2<-cnt2+1
setTxtProgressBar(pb, cnt2)
}
close(pb)
m[which(m==0)]<-NA
m2<-log(m)
dev.new()
par(mfrow=c(2,1))
par(mar=c(4.1,5.1,2.1,2.1))
image.plot(m2, axes=F,
breaks=seq(min(m2, na.rm=T),max(m2, na.rm=T),length=1000), col=rainbow(999),
xlab="Effect Size", ylab="P-value"
)
title(main=paste("n=",n))
axis(side=1, at=seq(0,1,by=.25), labels=seq(-4,4,by=2))
axis(side=2, at=seq(0,1,by=.05), labels=seq(0,1,by=.05))
axis(side=4, at =.5, labels="Log-Count", pos=.95, tick=F)
abline(h=.5, lwd=3, lty=1)
abline(h=.025, lwd=3, lty=2)
abline(v=.5, lwd=2, lty=1)
par(mar=c(5.1,4.1,4.1,2.1))
hist(p.out[which(p.out[,2]>.024 & p.out[,2]<.026),1],
xlim=c(-4,4), xlab="Effect Size", col=rgb(1,0,0,.5),
main=paste("Effect Sizes for","n=",n)
)
hist(p.out[which(p.out[,2]>(.499) & p.out[,2]<.501),1], add=T,
xlim=c(-4,4),col=rgb(0,0,1,.5)
)
legend("topleft", legend=c("0.499<p<0.501","0.024<p<0.026"),
col=c("Blue","Red"), lwd=3, bty="n")