I need to find a symmetric low-kurtosis distribution class, which includes the uniform, the triangular and the normal Gaussian distribution. The Irwin-Hall distribution (sum of standard uniform) offers this characteristic, but is not treating non-integer orders $N$. However, if you e.g. simply independently sum up e.g. 2 standard uniform $[0,1]$ and one 3rd with a smaller range like $[0,0.25]$ you will indeed nicely obtain a more general and smoothly extended version of Irwin-Hall for any arbitrary order (like $N=2.25$ in this case). However, I wonder if it is possible to find a practical closed formula for the CDF?
Asked
Active
Viewed 2,523 times
10
-
2"Smoothly extended" raises some thorny questions. In the thread at http://stats.stackexchange.com/questions/41467, the poster observes that the smoothness of the Irwin-Hall distribution changes abruptly from one (integral) value of $n$ to the next. This already suggests we should not expect there to be any mathematically "nice" closed form that is parameterized by real values of $n$. Moreover, there is no such closed formula even for the Irwin-Hall distribution itself. – whuber Oct 29 '13 at 14:28
-
1Hi, I made detailed sampling experiments and look to histograms of such generalized Irwin-Hall distribution. Indeed, introducing non-integer N helps to avoid jumps in the behavior! Also e.g. the kurtosis increases smoothly with real-valued N. If this would be not the case it would be indeed not nice. I think it should be possible to extend the Irwin-Hall summing formula for CDF in some way. – user32038 Oct 29 '13 at 14:46
-
1The summation is *not* a "closed formula" in the usual sense of the word because the number of terms increases without bound as $n$ varies. This is an important distinction, because true closed formulas do exist: the characteristic function of the Irwin-Hall distribution, $\left((\exp(it) - 1)/(it)\right)^n,$ exists for non-integral $n$ and so its inverse Fourier Transform answers your question--that is, if you consider that a closed *practical* formula! – whuber Oct 29 '13 at 15:09
-
1Hi whuber! I need a suitable implementation e.g. in Pascal. For moderate N (like 20) the well-known Irwin-Hall CDF formula is no problem at all, but I do not want to spend too much computing time, e.g. for an integration, (inverse) Fourier transform or whatever. Of course, the Fourier transform approach is elegant, but not so accurate, because I am highly interested in CDF(x) for "large" x, so the tail area matters for me! – user32038 Oct 29 '13 at 19:44
-
Hi, could you sketch our in more detail how you would go from Fourier transform of PDF to the plain CDF? (although I generally believe this method has oscillation problems in the tails, e.g. giving negative PDF if we try to evaluate the integral...). – user32038 Nov 04 '13 at 07:32
-
Indeed it does have oscillation problems. I mentioned that approach before you mentioned your interest in the tails, but even so analysis of the CF can provide information about asymptotic tail behavior. – whuber Nov 04 '13 at 20:18
-
Brian Ripley's simulation book does have a (complicated) closed exact formula! – kjetil b halvorsen Jan 02 '17 at 13:55
1 Answers
2
Well, this isn't really a full answer, will come back later to complete ...
Brian Ripley's book Stochastic simulation have the closed pdf formula as exercise 3.1 page 92 and is given below: $$ f(x) = \sum_{r=0}^{\lfloor x \rfloor} (-1)^r \binom{n}{r} (x-r)^{(n-1)}/ (n-1)! $$ An R implementation of this is below:
makeIH <- function(n) Vectorize( function(x) {
if (x < 0) return(0.0)
if (x > n) return(0.0)
X <- floor(x)
r <- seq(from=0, to=X)
s <- (-1)^r * choose(n, r)*(x-r)^(n-1)/factorial(n-1)
sum(s)
} )
which is used this way:
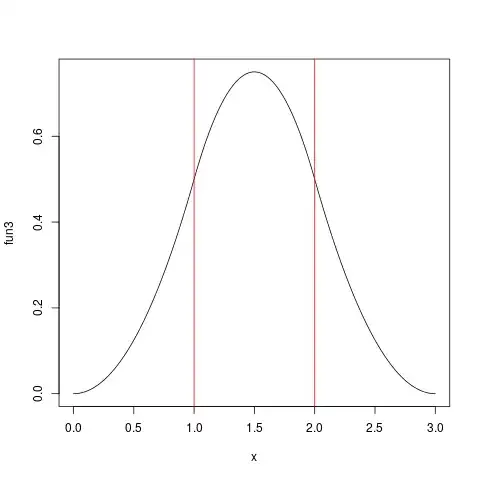
fun3 <- makeIH(3)
plot(fun3,from=0,to=3,n=1001)
abline(v=1, col="red")
abline(v=2, col="red")
and gives this plot:
The unsmoothness at the integer values $x=1, x=2$ can be seen, at least with a good eyesight ....
(I will come back to complete this later)
kjetil b halvorsen
- 63,378
- 26
- 142
- 467
-
1+1 I'd be interested in seeing what the completion of this is, if you have time. ... As an aside, while I know that there's a lack of smoothness here (in the sense of there being discontinuities in the second derivative) I can't say that I really perceive it as not-smooth (my eye tends to say "no kinks, it looks smooth"). I assume that if I was riding a roller coaster along that curve, I'd be sure to *feel* the change though. – Glen_b Mar 13 '17 at 21:31
-
-
Too see the lack of smoothness probably we will need to choose the plotting points to include the integers ... – kjetil b halvorsen Nov 13 '18 at 13:30