2

I am new to statistics and have run into some trouble understanding computing confidence intervals and am seeking some help. I will outline the motivating example in my textbook and hopefully someone can offer some guidance.

Example

There is a population of mean values and your goal is to figure out the true mean (as best you can). In order to accomplish this, a number of samples are taken, each of which has a mean value.

Next, because we know by the central limit theorem that as the number of samples increase, the sampling distribution will be normally distributed, we use the equation $z = \frac{X - \bar{X}}{s}$ (noting that in this case s = standard error) to compute a lower and upper bound taking each sample mean as the mean for the z-score equation and z-scores of -1.96 and +1.96, for example, to compute a 95% confidence interval.

I’ve included a graph from my textbook in attempt to add clarity.

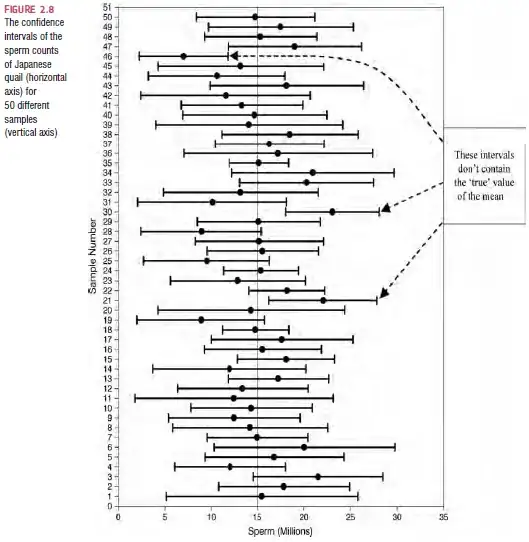
enter image description here

So I do not understand how it is you can use each sample mean as the mean value in our z equation to compute intervals. We know that the sample distribution is normally distributed so isn’t it the case that only the mean of all the samples can be used? How can we compute an interval around each mean value that contributes to the sampling distribution?

Any help with this would be much appreciated

Note: I'm reading "Discovering Statistics Using IBM SPSS Statistics 3rd Edition" by Andy Field and this example is from pg 43-45

Amateur Math Guy
  • 123
  • 4
  • You can learn a lot about confidence intervals by [searching our site](http://stats.stackexchange.com/questions/6652/what-precisely-is-a-confidence-interval). Please note that the CLT does *not* assert the sampling distribution of the mean will become Normal as the number of samples increases: it only says something about the distribution when the *sample sizes* increase. – whuber Oct 27 '13 at 15:30
  • I tried looking at the answers to the link you posted and am still confused (some of those answers seem to be a little over my head at this early point in my learning statistics for fun). Can you explain a little more about how it is that the standard error will be used in computing the interval in each case, and that comes from all the samples (ie the standard deviation of sample means i think), and yet the mean value used is specific to the individual sample. I'm just having trouble understanding how everything fits together – Amateur Math Guy Oct 27 '13 at 22:30
  • 1
    You seem to be assuming all those samples are available to the person computing the interval. This suggests you didn't understand the point of the example whose only aim was to explain the meaning of a CI computed from a single sample. The situation is there's ONE sample available and one computes a CI for the population mean from it... but what is the meaning - as a probability statement - of the "95%"? The explanation of what that interval *means* is in terms of other samples that might have been available (to the individual computing their interval), but presently aren't. – Glen_b Oct 27 '13 at 23:00
  • 1
    As you can tell from @Glen_b's comment, we are sympathetic. But what is needed to re-open the question is an edit to the question itself that clearly differentiates it from the apparent duplicates. Do you think you could identify a little more specifically what your problem is? I think most would-be answerers would struggle trying to respond to the query concerning "how everything fits together," especially because CIs have been described in such detail at so many different levels throughout this site. – whuber Oct 28 '13 at 13:15

0 Answers0