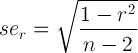Standard error from correlation coefficient

Question

Many studies only report the relationship between two variables (e.g. linear or logistic equation), $n$, and $r^2$. I want to use these reported statistics to reproduce this relationship with its variation. Most statistical software will generate a parameter distribution from a mean and standard error. Assuming a normal distribution, can the standard error of the parameter estimates be calculated with just these three statistics? Essentially, can I get a standard error from $r^2$?

Or will I need to do some kind of bootstrapping procedure to generate a distribution that has the same $r^2$ and then calculate the standard error? if so are there better ones for linear vs. nonlinear equations?

Answer 1

If you look at the Wikipedia page for the Pearson product-moment correlation, you will find sections that describe how confidence intervals can be calculated. Typically, people will use Fisher's $z$-transformation (arctan) to turn the $r$ into a variable that is approximately normally distributed:
$$ z_r = \frac 1 2 \ln \frac{1 + r}{1 - r} $$ Having applied this transformation, the standard error will be approximately $^1/_{\sqrt{(N-3)}}$. With this you can form whatever length confidence interval you like. Once you've found the confidence limits you want, you can back-transform them to the original $r$ scale (i.e., $[-1, 1]$) like so:
$$ \text{CI limit}_r = \frac{\exp(2z) - 1}{\exp(2z) + 1} $$ In other words, you can form a confidence interval for $r$ without the original data, so long as you have the original $N$.

_{Notes: This approach is an approximation, there are exact formulae listed on the Wikipedia page, but they are harder to use. Although it doesn't say on the Wikipedia page, there are several conditions you want to meet in order for this approximation to be reasonable. The $N$ should be at least $30$ (IIRC), and the marginal distributions (i.e., the univariate distributions of the two variables being correlated) should be normal. For example, I'm not sure that this will be accurate if the correlation were composed of two vectors of $1$s and $0$s. However, higher $N$ should allow you to compensate for minor non-normality.}

Answer 2

To add to gung's answer, one can also use the a lazy approach of directly calculating the standard error for the correlation. This will produce inaccurate results in some cases and may produce impossible out of range confidence intervals. But for most cases, it's fine. The equation is:

Example calculation of confidence interval

Assume that n=200, r=.3. I use the CIr function from psychometric to get the CIs based on Fisher's Z transformation. Then I calculate the standard error of the correlation based on the direct approach and find the same CI (95%):

> psychometric::CIr(.3, 200)
[1] 0.17 0.42
> sqrt((1-.3^2)/(200-2))
[1] 0.068
> .3 - 1.96 * 0.068
[1] 0.17
> .3 + 1.96 * 0.068
[1] 0.43

.17-.42 vs. .17-.43. Thus, we see that the approaches yield only a minor difference.

The quick method gets more inaccurate the closer the |correlation| gets to 1 and with small n's. To illustrate, assume now that n=20, r=.9. Then:

> psychometric::CIr(.9, 20)
[1] 0.76 0.96
> sqrt((1-.9^2)/(20-2))
[1] 0.1
> .9 + 1.96 * 0.1
[1] 1.1
> .9 - 1.96 * 0.1
[1] 0.7

So, here the results are markedly different: .76-.96 vs. .7-.1.1! The latter is impossible, so we could reduce to .7-1.0. The two plots below show the difference in the lower and upper limits, respectively:

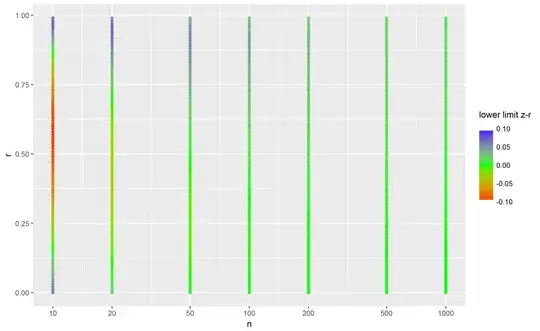
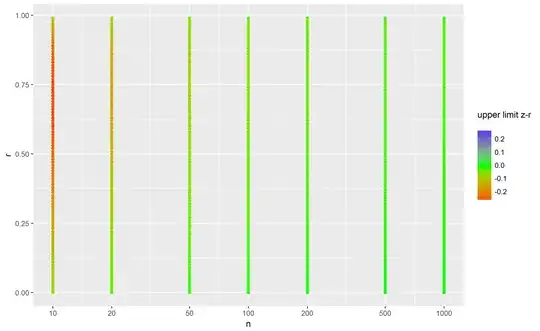
So, blue indicates that the quick method produced too low values, red that it produced too high values and green when it gave correct answers. My takeaway is that when n is below 100, the quick method gives pretty imprecise results, but for larger n's, it doesn't matter so much.

The equation is given in e.g.:

Cohen, J., & Cohen, J. (Eds.). (2003). Applied multiple regression/correlation analysis for the behavioral sciences (3rd ed). Mahwah, N.J: L. Erlbaum Associates.

See also this question on SO.