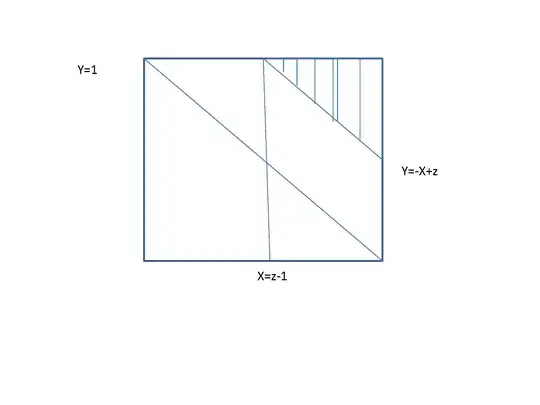
Consider the following short example of transformations.
Let the joint density of X and Y be given by the unit square, i.e.
$$f_{X,Y}(x,y) = \begin{cases} 1\ \quad 0<x<1\ \text{ and }\ 0<y<1 \\ 0 \quad \text{elsewhere} \end{cases}$$
Then the Cumulative Distribution Function of $Z=X+Y$ is given by:
$$ F_Z = \begin{cases}\begin{array}{ll} 0\ & \text{ for }\ z<0 \\ \int_0^{z} \int_0^{z-x} dy\,dx\ & \text{ for }\ 0\leq z <1 \\1-\int_{z-1}^1 \int_{z-x}^1 dy\,dx\ & \text{ for }\ 1\leq z<2 \\1\ & \text{ for }\ 2\leq{z} \end{array}\end{cases} $$
I understand why we have to partition our CDF, what I am having trouble figuring out is why for the interval $[1,2)$ that specific form. What is the intuition here? Thanks.