The simple difference between the two is that the posterior distribution depends on the unknown parameter $\theta$, i.e., the posterior distribution is:
$$p(\theta|x)=c\times p(x|\theta)p(\theta)$$
where $c$ is the normalizing constant.
While on the other hand, the posterior predictive distribution does not depend on the unknown parameter $\theta$ because it has been integrated out, i.e., the posterior predictive distribution is:
$$p(x^*|x)=\int_\Theta c\times p(x^*,\theta|x)d\theta=\int_\Theta c\times p(x^*|\theta)p(\theta|x)d\theta$$
where $x^*$ is a new unobserved random variable and is independent of $x$.
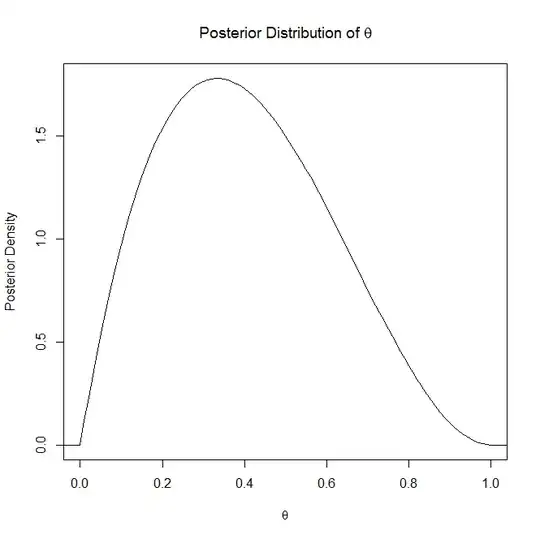
I won't dwell on the posterior distribution explanation since you say you understand it but the posterior distribution "is the distribution of an unknown quantity, treated as a random variable, conditional on the evidence obtained" (Wikipedia). So basically its the distribution that explains your unknown, random, parameter.
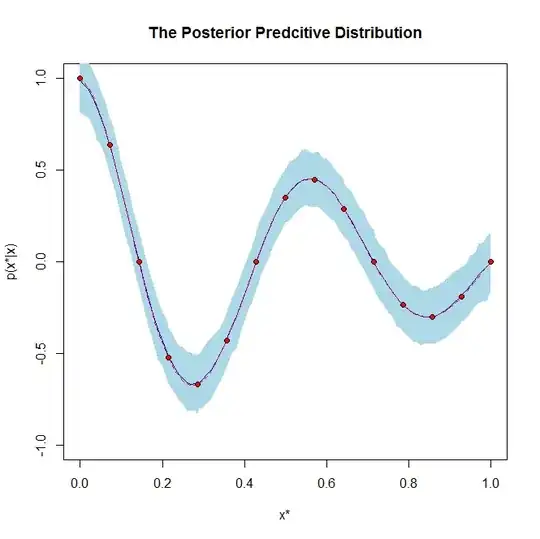
On the other hand, the posterior predictive distribution has a completely different meaning in that it is the distribution for future predicted data based on the data you have already seen. So the posterior predictive distribution is basically used to predict new data values.
If it helps, is an example graph of a posterior distribution and a posterior predictive distribution: