4

Say I have $n$ independent observation of two random variables $x$ and $y$, which may be correlated, and I want to estimate $r=E[x/y]$.

I can use $\bar{r}=\sum_i \frac{x_i}{y_i}$ to estimate $r$ but how do I determine confidence intervals?

Edit: a single observation is of the type $(x_i,y_i)$ and obviously I can compute $r_i=x_i/y_i$ for all observations. Should I just compute the classic confidence interval for $r_i$?

algebrain
  • 41
  • 2
  • Putting $z=\frac{x}{y}$ you ask about a nonparametric confidence interval of $E[z]$. I think the fact that $z=\frac{x}{y}$ is useless in this problem. – Stéphane Laurent Sep 06 '13 at 17:59
  • Please check your formula for $\bar r$. Also your notation appears to use $r$ both for sample and population quantities; I strongly suggest you avoid doing that. Appropriate estimates and confidence intervals for the population $r$ depends on things not specified here. For example if $x$ and $y$ are bounded to be positive we'd expect the variance to be related to the mean, in which case the intervals will be biased when you treat the variance of $r_i$ as constant. – Glen_b Sep 07 '13 at 00:14
  • Glen, yes x and y are both positive. Why should bootstrapping as suggested by soakley not work in this case? I imagine you refer to finding an asymptotic closed-form result for the interval. (sorry for messing up notation. I'm not a statistician) – algebrain Sep 09 '13 at 10:17
  • Stephane, are you saying that I can just define a new variable z=x/y and look directly at its variance? Instead, things would be more complicated if I was looking to estimate the confidence interval for an estimation of E[x]/E[y]. Am I right? – algebrain Sep 09 '13 at 10:58
  • @Glen_b: If the sample size is large enough, a simple z-confidence interval is still an option: The $(x,y)$-pairs are sampled independently from the same bivariate distribution. Thus, true mean and variance of the considered ratio are constant, although possibly related. – Michael M Oct 11 '13 at 12:30

2 Answers2

1

I'm not an expert in statistics as well, but I recently read the excellent book by Efron/Tibshirani (1997) and the bootstrap is a quite capable tool of questions such as yours. As pointed out here in the excellent answer by cardinal, the bootstrap really doesn't need specific assumptions, but performs very well quite generally.

With respect to your problem, this means that it can help to just run a bootstrap. I'm gonna do this here in R:

#Load required packages
library(boot)
library(MASS) #To simulate multivariate normally distributed observations
set.seed(369)

#Run bootstrap in the case of a positive correlation between x and y
N <- 1e4
X <- mvrnorm(N, mu=c(100,20),
             Sigma = diag(c(20,5)) %*% matrix(c(1,0.9,0.9,1), nrow=2) %*% diag(c(20, 5)))
r <- X[,1]/X[,2]


b_pos <- boot(data=r,
          statistic=function(x, i) mean(x[i]),
          R=5000)
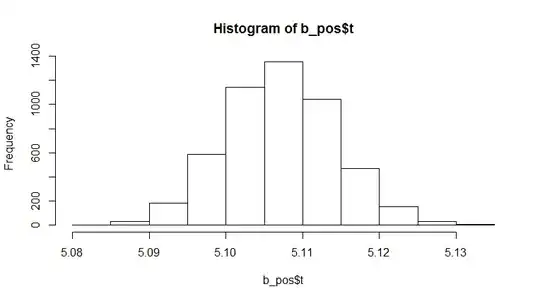
hist(b_pos$t)

enter image description here

#Run bootstrap in the case of a negative correlation between x and y
X <- mvrnorm(N, mu=c(100,20),
             Sigma = diag(c(20,5)) %*% matrix(c(1,-0.95,-0.95,1), nrow=2) %*% diag(c(20, 5)))
r <- X[,1]/X[,2]

b_neg <- boot(data=r,
          statistic=function(x, i) mean(x[i]),
          R=5000)
hist(b_neg$t)

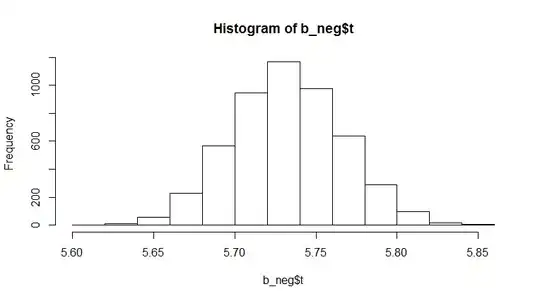
enter image description here

So what I find interesting here is the fact that the distribution seems to be shifted to the right with a decreasing correlation between $x$ and $y$. However, the mean always seems to be above $E[x]/E[y]$ which would be 5 in this case. (Note that $x$/$y$ is normally distributed with mean 100/20 and standard deviation of 20/5 here. I'm pretty sure that this result can be derived analytically quite easily for a trained statistician, but that's the beauty of the bootstrap: Even people without that background knowledge can get a fast feeling for the distribution of any statistic (and even trained statistician are often unable to derive distributional forms because there simply doesn't exist an analytical solution).

Now it's also easy to adjust the example to find out how $E[x]/E[y]$ behaves:

b_alt <- boot(data=X,
              statistic=function(x, i) mean(X[i, 1])/mean(X[i,2]),
              R=5000)
hist(b_alt$t)

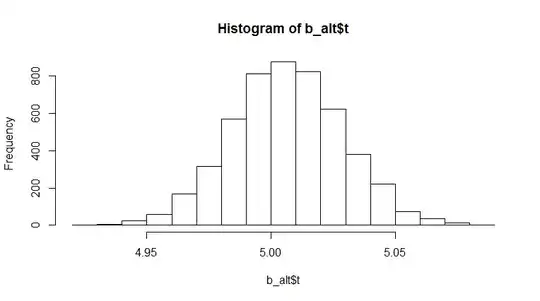
enter image description here

This is just centered around 100/20=5 as expected. Note, however, that things change quite dramatically if you center both variables around 0. Then, $E[x]/E[y]$ is not well-behaved anymore because the the denominator end up very close to zero quite often, whereby $E[x/y]$ first calculates the ratios and then averages, which averages the outliers.

Community
  • 1
Christoph_J
  • 868
  • 1
  • 9
  • 18
0

Try resampling. So you take, say 10,000 samples (with replacement) of size $n$ and compute the empirical averages as you did in your original sample. Sort the 10,000 averages, then throw out the smallest 250 and the largest 250. The range of the remaining realizations is a 95% confidence interval.

soakley
  • 4,341
  • 3
  • 16
  • 27
  • Thanks. This actually sounds like a very general method to compute confidence interval for any sort of statistic. What are pros and cons versus relying on CLT? I have a rather small sample. – algebrain Sep 06 '13 at 17:33
  • I like that it's nonparametric, but if you have previous knowledge this may not be an advantage. Personally, I would do both the resampling and the traditional confidence interval. Many times they will be consistent with each other. – soakley Sep 06 '13 at 20:02