Detect weak points of change (temperature profile)

Question

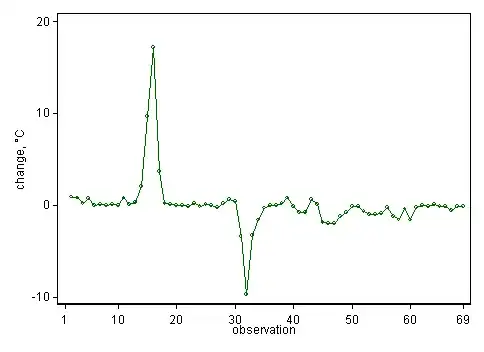
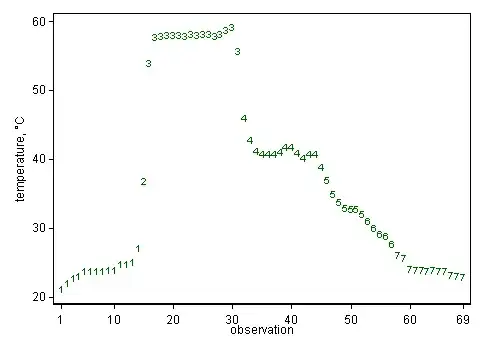
I am working on a method to detect a finite set of significant points of temperature change within a data series. Although my first pass does an okay job of detecting significant temperature transitions, the results are less than ideal when working with a noisy signal or weak temperature variance.

Sample Temperature Profiles

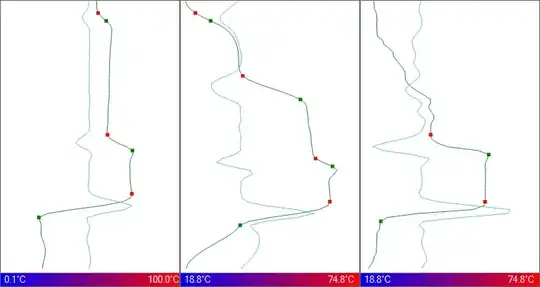
The X axis represents temperature and Y represents a sensor reading within the data set

Current Approach

1. Apply Savitzky–Golay Filter using multiple passes with a small window size to smooth data.
2. Calculate rate of change on smoothed data series and calculate standard deviation.
3. Starting with z-Score of 1.96 (~95% confidence) slowly increase or decrease confidence until I locate 2-5 significant temperature shifts that best fit the result of the previous data series or give up if I reach 0.84 (~60% confidence).

As illustrated in the left and middle profiles, this works okay; however there are times like the right profile where I need to detect changes in temperature that are weaker than my minimum allowed confidence of 60%. I know I could just continue to lower the bar (i.e., 50% or lower), but I am hoping there is a better approach.

Changes Considered

1. Reduce the minimum confidence level to 50% or lower to detect weaker transitions.
2. Given that there is normally a significant temperature increase on the lower half of the profile; break the data up into two halves at the maximum temperature reading (idea being variance on top half is typically weaker than the bottom half).
3. Don't use standard deviation and find the most significant transitions by identifying peaks and valleys ranked by overall temperature change.
4. Other…

---

I have been reading a lot of the related questions as well as scouring Wikipedia. I am fairly certain this is a well understood problem, and I am hoping someone can point me in the right direction on how to correctly identify the most significant changes in temperature given a small data series (72-120 values) while dealing with noise and weak variance.

---

EDIT 1

I neglected to mention that one of the challenges I am currently facing is that by applying the smoothing filter, I am negatively affecting my ability to detect weaker points of significant change.

---

EDIT 2

A raw sample data series (°C) representing the right temperature profile if needed…

21.00,  21.90,  22.70,  22.90,  23.60,  23.60,  23.70,  23.70,  23.80,  23.80,   24.60,  24.70,  25.00,  27.00,  36.70,  53.90,  57.60,  57.80,  57.90,  57.90,  57.90,  57.80,  58.00,  57.90,  58.00,  58.00,  57.80,  58.00,  58.60,  59.00,  55.60,  45.90,  42.60,  41.00,  40.70,  40.70,  40.70,  40.90,  41.70,  41.60,  40.80,  40.00,  40.60,  40.70,  38.80,  36.80,  34.80,  33.60,  32.80,  32.70,  32.60,  31.90,  30.90,  29.90,  29.00,  28.80,  27.60,  26.00,  25.60,  24.00,  23.80,  23.80,  23.70,  23.80,  23.70,  23.60,  23.00,  22.90,  22.80

Answer 1

Various comments:

• Your discussion is free with technical words such as "significance" and "confidence", but note that the relationship with the formal senses of those terms is tenuous. In particular, you have no formally defined generating process and your use of multipliers based on standard normal distributions includes no adjustments for dependence structure, either in your raw data or as smoothed. I don't have concrete suggestions for alternative inference procedures, not least because it seems that you are much better off regarding what you do as just exploratory or heuristic. But it's best in any report to put " " around those terms at least once, or even to avoid them altogether. Note that in my view exploratory and heuristic are not dirty words. Finding structure in data is one of the most vital parts of statistical science.

• A heuristic of smoothing the data a little and then looking for jumps in the smoothed series sounds a good idea, although what you are doing already sounds a bit too complicated. Much depends on the sociology of your situation, i.e. who you have to explain this to and what they will understand or expect.

• Your method of presenting the data and your general pitch implies to me that you are looking at temperature changes with depth e.g. below the land surface. If so, beware anyone trying to sell you anything based on time series analysis, as if these data are spatial, heat can (presumably) be propagated in both directions, unlike a time series in which past and future are quite unequal.

• A simple exploratory plot of one-step temperature changes (temperature $-$ previous temperature) in your sample series suggests that most of the biggest temperature changes are short ramps over 2-3 or so intervals. You may be able to relate that to the physics of your problem. This may have implications for your degree of smoothing, for example implying that Savitzky-Golay smoothing smooths too much.

• Much depends on your relative emphasis on (a) detecting jumps as compared with say (b) detecting zones or epochs within which temperature (or temperature change) is approximately constant. There are literatures on both. For example, a previous thread at How can I group numerical data into naturally forming "brackets"? (e.g. income) describes procedures for dividing series into subseries. You get to choose on the trade-off between number of subseries and internal homogeneity. Here is an arbitrary sample result from such a procedure. The criterion was to look for subseries with minimum internal variability in temperature, as defined by a sum of squared deviations from the mean. The numerals 1, ..., 7 indicate subseries identified. You could apply the same method to temperature change, or any other series.