I am looking for some help with my time-series data. What is the best method of detrending/transformation of these two variables, so I do not violate assumptions of stationarity when applying a cross correlation function (to find out if one series is leading the other)?
The cross correlation function shows that the raw series are correlated when HDA is shifted back two year, but applying this without transformation of data and error structure would be wrong. Because I am working with scaled variables from 0 to 1 and because my x variable contains zeroes, I am not sure what is the best way to go about this (I can correct for non-constant mean via OLS detrending, but don't know how to address non-constant variance and non-independence of errors). Could this type of question be answered with wavelets?
The y variable is a time series of biomass (B) scaled to the maximum value of B. The x variable is a time series of the proportion of high density areas (HDA), scaled to the maximum value of HDA
y<-c(0.84685420,0.64096448, 0.61250603, 0.49262176, 0.34298023, 0.39499759, 0.23326153, 0.27661148, 0.52848738, 0.66898569, 0.71739592, 0.74696673, 0.78385469, 0.92071371, 0.96981193, 1.00000000, 0.95564700, 0.83825109, 0.67275358, 0.59576917, 0.42636232, 0.33447999, 0.30739109, 0.14768687, 0.14132776, 0.08885388, 0.07370519, 0.08349140, 0.05824787, 0.04986337, 0.04616621, 0.04828163, 0.04666131, 0.02836843, 0.03283073, 0.09343192, 0.06804694, 0.06146279, 0.12578685, 0.17464716, 0.30159781, 0.33469217)
year<-c(1970:2011)
x<-c(0.00000000, 0.27272727, 0.09297521, 0.53827751, 0.17786561, 0.09977827, 0.10765550, 0.49889135, 0.29933481, 0.77922078, 0.85623679, 1.00000000, 0.47568710, 0.97402597, 0.39430449, 0.56426332, 0.31774051, 0.47661077, 0.27579162, 0.46487603, 0.38654259, 0.31168831, 0.15151515, 0.15293118, 0.00000000, 0.22113022, 0.00000000, 0.00000000, 0.16201620, 0.15437393, 0.00000000, 0.14229249, 0.00000000, 0.00000000, 0.00000000, 0.00000000, 0.14354067, 0.08704062, 0.00000000, 0.23830538, 0.07718696, 0.05928854)
ccf<-ccf(x,y,type="correlation", main="x=HDA/max(HDA), y=B/max(B)", ylab="ccf")
original biomass is
y<-c(131707, 99686, 95260, 76615, 53342, 61432, 36278, 43020, 82193, 104044, 111573, 116172,121909, 143194, 150830, 155525, 148627, 130369, 104630, 92657, 66310, 52020, 47807, 22969,21980,13819,11463,12985,9059,7755,7180,7509,7257,4412,5106,14531,10583, 9559,19563, 27162,46906, 52053)
logy<-log(y)
and I am looking at the scaled biomass so then that would be
logy.scaled<-logy/max(logy)
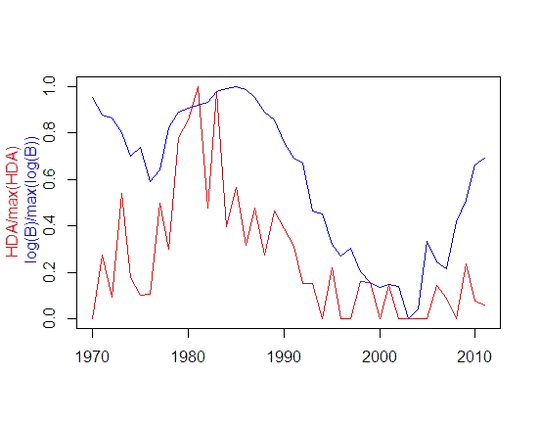
what would be the best way to apply a ccf? or other method to see the red series leads the blue in time?