Two player dice game probability

Question

$A$ and $B$ play a dice game where a player wins if their score is higher. $B$ wins if their score is equal. What is the probability of $A$ winning if both the players roll their dice $n$ times and choose their best scores (out of their $n$ throws)?

Answer 1

For a particular die roll the cumulative probability is $ P(X_i \leq x ) = x/6 $, for $x=1,...,6$. So, if the die rolls are independent,

$$ P(\max \{ X_1, ..., X_n \} \leq m) = P(X_1 \leq m, ..., X_n \leq m) = \prod_{i=1}^{n} P(X_i \leq m ) = \left( \frac{m}{6} \right)^n $$

for $m=1,...,6$. When $m > 6$ this probability is clearly $1$ and $0$ if $m < 1$.

From this it's simple to deduce that $$P(\max \{ X_1, ..., X_n \} = m) = \frac{m^n - (m-1)^n}{6^n} $$

(I've suppressed the indicator that $m \in \{1,...,6\}$). Note that to generalize this to a $k$-sided die, just replace $6$ everywhere with $k$.

---

Suppose players $A$ and $B$ throw the die $n_A$,$n_B$ times with maximum rolls $M_A, M_B$, respectively. By the description above, player $A$ wins if $M_A > M_B$. Using the law of total probability,

\begin{align*} P(M_A > M_B) &= E_{m} \Big( P(M_A > M_B | M_B = m) \Big) \\ &= E_{m} \Big(1 - \Big( \frac{m}{6} \Big)^{n_A} \Big) \\ &= \frac{1}{6^{n_A + n_B}} \sum_{m=1}^{6} \left(6^{n_A} - m^{n_A} \right) \left(m^{n_B} - (m-1)^{n_B} \right) \end{align*}

If $n_A = n_B = n$, this simplifies to

$$ \frac{1}{6^{2n}}\sum_{m=1}^{6} \left(6^n - m^n \right) \left(m^n - (m-1)^n \right) $$

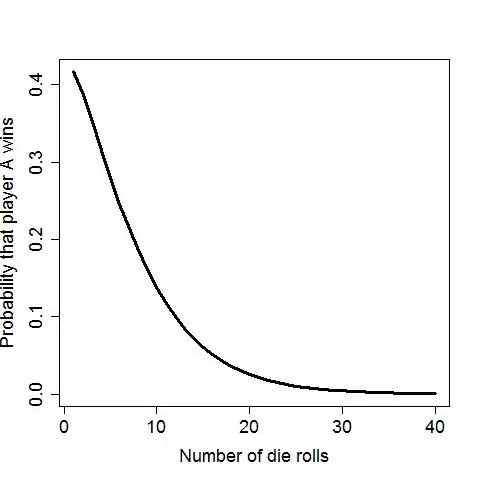
Below this is plotted as a function of $n$. In this example, it's intuitive that the probability of $A$ winning quickly goes to zero as $n$ increases since their maximums become increasingly likely to both be six, in which case $B$ wins.

$ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ $