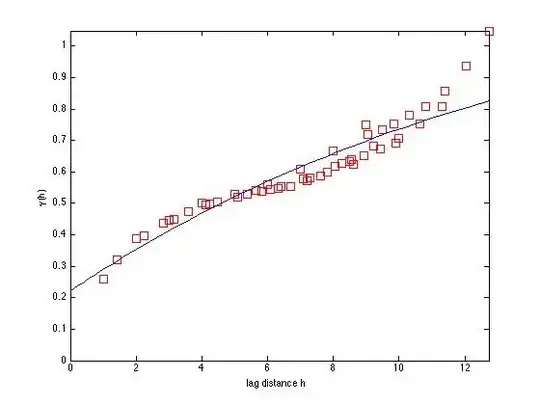
I am trying to fit a spherical variogram to some synthetic data using the code available at http://www.mathworks.com/matlabcentral/fileexchange/25948-variogramfit. However, I have some doubts. I simulated some synthetic data using GMRF with the defined graph structure. I mean, I generated some samples where each sample is a multivariate gaussian distribution over space. I then took pairwise semi variances and got the overall semivariogram.
I then fit the model variogram to this empirical one. This is what I got. However, I have some doubts, when I generated the synthetic data it had no noise. So I was assuming no nugget effect. However, I am seeing significant nugget effect why is it so. I just drew samples from a multivariate gaussian distribution over space.
I have a spatial grid of size 10x10, the variables in this form a multivariate gaussian distribution. Any suggestions?
I am not sure but the more samples I add, and calculate the pair wise semi variance, the nugget starts increasing. Even though the empirical semi variogram is smoother, the nugget starts appearing more. What is the reason behind this?