The main work-horse behind the computation of SVD is the QR algorithm. Having said that there are many different algorithms to calculate the singular value decomposition of a generic $M$-by-$N$ matrix $A$. A great schematic on the issue available here (from the documentation of Intel's MKL) is the following: 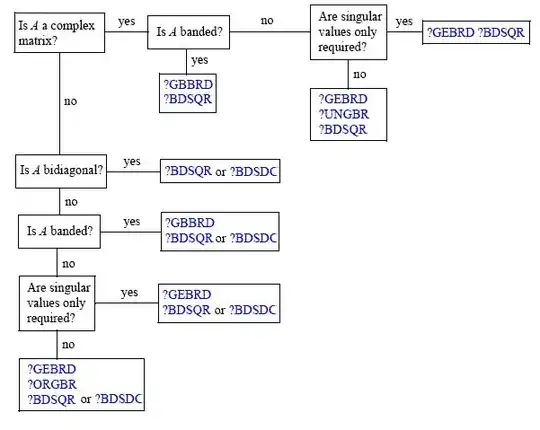
As you see depending on your use case there are different approaches (the routine naming conventions can be found here). That is because, for example there are matrix forms where a Householder reduction can be more expensive than a Givens rotation (to name two "obvious" way of getting QR). A standard reference on the matter is Golub's and Van Loan's Matrix Computations (I would suggest using at least the 3rd edition). I have also found Å. Björck's Numerical Methods for Least Squares Problems very good resource on that matter; while SVD is not the primary focus of the book it helps contextualizing the use it.
If I have to give you one general advice on the matter is do not try to write your own SVD algorithms unless you have successfully taken a couple of classes on Numerical Linear Algebra already and you know what you are doing. I know it sounds counter-intuitive but really, there as a tonne of stuff that can go wrong and you ending up with (at best) sub-optimal implementations (if not wrong). There some very good free suites on the matter (eg. Eigen, Armadillo and Trilinos to name a few.)
