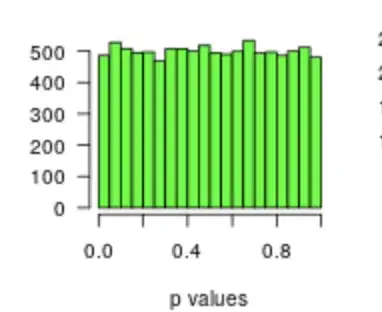
Inspired by this: http://pss.sagepub.com/content/22/11/1359
In the context of open-ended data collection where the necessary sample size cannot be properly estimated, for the purpose of a frequentists test;
I understand that a stopping condition based on the main outcome is circular. For example, if I stop sampling once my p value happens to be below .05, my p value is biased (so much as to be mostly worthless). However, say I choose another stopping rule, such as the width of my 95% confidence interval (without regard for other aspects of the test, such as e.g. if the CI includes 0), am I introducing any bias (but for, of course, CI width and related statistics)?
As far as I understand it, this is not a problem in a Bayesian analysis, but I am wondering about the options for conditional stopping precluding frequentist tests.