Distribution fitting problem

Question

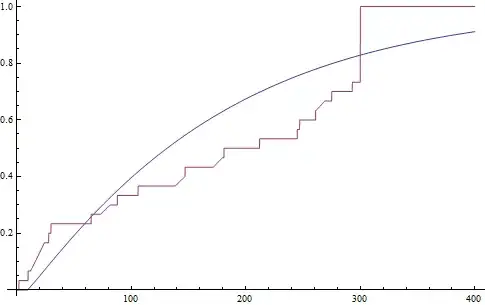
I have a real data set 275, 13, 147, 23, 181, 30, 65, 10, 300, 173, 106, 300, 300, 212, 300, 300, 300, 2, 261, 293, 88, 247, 28, 143, 300, 23, 300, 80, 245, 266 and try to fit a Weibull distribution using Maximum Likelihood. I used Mathematica for analysis and Mathematica gives me the parameter estimates of Weibull distribution as $\alpha=1.07484, \beta=171.242,\gamma=9.46641$ where $\alpha,\beta$ and $\gamma$ are the shape, scale and location parameters, respectively. Now my two questions are:

If I find CDF of Weibull distribution using estimated parameters for minimum value of data set answer is Zero which is obvious but for maximum value the answer become 0.828829 Why it is not One?
How I find the estimated value using these parameter estimates?

Note. Question 1 problem also occurs for other distributions as well; here the Weibull distribution is taken as an example. Mathematica code's and result are here

This is normal. In this case, the CDF of the Weibull distribution goes to 1 as $x$ goes to infinity. The [*empirical CDF*](http://en.wikipedia.org/wiki/Empirical_distribution_function) is 1 for the maximum value in your dataset: `DiscretePlot[CDF[EmpiricalDistribution[data1], x], {x, 0, 400}]`. If you use MLE to estimate the parameters of a theoretical distribution, the CDF of this distribution is not limited to your data set. I don't understand the second question. What do to you mean by "estimated value"? — COOLSerdash, Jul 18 '13 at 08:27
Not your question, but 8/30 values in your data are equal to the maximum 300. You are evidently fitting a three-parameter version of the Weibull, but even so, these data don't look like a good candidate for such a distribution. Some kind of censoring issue? — Nick Cox, Jul 18 '13 at 08:32
@COOLSerdash: The maximum value of data set is `300` not `400`. If it is so why it is exactly zero for `2` minimum value in general it is for `0` and for second question estimated values mean fitted values closest to observed value, to compare the actual value and fitted value's. — SAAN, Jul 18 '13 at 08:41
@NickCox I also try it for two parameter Weibull, the result of CDF is round 0.83, so not much difference. I also write in Question Weibull is taken as an example I also try on other distribution e.g inverse Weibull, generalized Weibull etc. but same problem occur. But if we go back in Graduate classes where the sum of the probabilities is one. — SAAN, Jul 18 '13 at 08:48
Total probability being 1 taught in elementary school now? More seriously, I don't see why you are puzzled or surprised here. Any distribution without a finite upper bound will give a finite estimated probability for values being greater than the sample maximum. I don't know how seriously you take your example, but it's pathological given the spike of tied maxima. — Nick Cox, Jul 18 '13 at 09:18
Azeem I am well aware that the maximum of your data set is 300. The 400 is the limitation of the plot (did you even run it?). Again: This is *not* a problem but an expected result. Why do you think that the CDF should be 1 for your maximum value? The support of your fitted distribution is $(\gamma, +\infty)$ (i.e. it has probability zero when $x\leq\gamma$). This means that the CDF is an integral of the PDF from $\gamma$ to $+\infty$. This means the CDF approaches 1 if $x\rightarrow+\infty$. — COOLSerdash, Jul 18 '13 at 09:18
My basic aim is to show how much Weibull distribution fits data well, it may be in term of probabilities or values. In my thinking it will be empirical probabilities vs CDF of fitted or Actual vs fitted values. — SAAN, Jul 18 '13 at 09:46
@COOLSerdash please look also `DiscretePlot[CDF[EmpiricalDistribution[data1], x], {x, 0, 300}]` and `DiscretePlot[CDF[EmpiricalDistribution[data1], x], {x, 2, 300}]` — SAAN, Jul 18 '13 at 09:48
@NickCox agreed, I am surprised for minimum value it is 2 and CDF answer is exactly zero, it is also hold for less then 10. — SAAN, Jul 18 '13 at 09:57

score 2 · Accepted Answer · answered Jul 18 '13 at 10:02

2

I'm posting this as an answer because I want to include a graphic for illustration. Azeem: Look the fitted Weibull CDF and compare it to the empirical CDF:

data1 = {275, 13, 147, 23, 181, 30, 65, 10, 300, 173, 106, 300, 300, 
  212, 300, 300, 300, 2, 261, 293, 88, 247, 28, 143, 300, 23, 300, 80,
   245, 266}

param = FindDistributionParameters[data1, 
  WeibullDistribution[a, b, c]]

Plot[{CDF[WeibullDistribution[a, b, c] /. param, x], 
  CDF[EmpiricalDistribution[data1], x]}, {x, 0, 400}, 
 Exclusions -> None]

WeibullFit

The fit doesn't look very good. Also, what about @Nick's point about the excess values of 300? Could you please explain how these data were collected? What do they represent?

answered Jul 18 '13 at 10:02

COOLSerdash

25,317
8
73
123

Thanks for the Answer, Yes Using Likelihood ratio criterion I already know Weibull distribution not fit it well, for research purpose I have modified Weibull distribution which fits better, now I easily adds new distribution fit on it. Thats exactly what I want. – SAAN Jul 18 '13 at 10:11
I don't use Mathematica, but a fit that gives a fitted minimum less than the observed minimum seems dubious. – Nick Cox Jul 18 '13 at 10:17
@COOlSerdash The data set studied by Meeker and Escobar (1998, p. 383), which gives failure times for a sample of devices from a field-tracking study of a larger system. At a certain point in time, 30 units were installed in normal service conditions. Two causes of failure were observed for each failed unit: the failure caused by an accumulation of randomly occurring damage from power-line voltage spikes during electric storms and failure caused by normal product wear. – SAAN Jul 18 '13 at 10:19
@NickCox please keep in mind Weibull distribution is taken as an example. Actual distribution is complicated thats why not consider here. – SAAN Jul 18 '13 at 10:23
1. You are missing my point. If a program ever estimates a location parameter contradicted by the data, what is going on? – Nick Cox Jul 18 '13 at 10:27
2

2. This site is not just about answering individuals' questions in public but about providing a resource for others to use later. Only the examples you give can be discussed; referring to other examples we can't see is of no use or interest to anybody. – Nick Cox Jul 18 '13 at 10:29
2

3. Meeker and Escobar (1998) is not a full reference. I'd guess that the values of 300 were censored, i.e. failures not observed at time 300. – Nick Cox Jul 18 '13 at 10:30
@NickCox I've checked the fitting solution with different starting values. The estimated parameters are highly sensitive to the starting values. For me, this just indicates that a 3-parameter Weibull is ill-advised for these data. – COOLSerdash Jul 18 '13 at 10:43
2

Statistical Methods for Reliability Data by William Q. Meeker and Luis A. Escobar, published by John Wiley & Sons, 1998. – SAAN Jul 18 '13 at 10:43

Distribution fitting problem

1 Answers1

Linked