I have carried out cluster analysis and now want to compare means between variables in different clusters. The variables in question are age and expenditure in millions of dollars.
The age variable does not follow a normal distribution: as a result, I was considering a Mann-Whitney test. The expenditure in millions of dollars fails the assumption of equality of variances.
Having stated this, although all tests seem to suggest that age does not follow normal distribution, I am not quite sure about the extent of this.
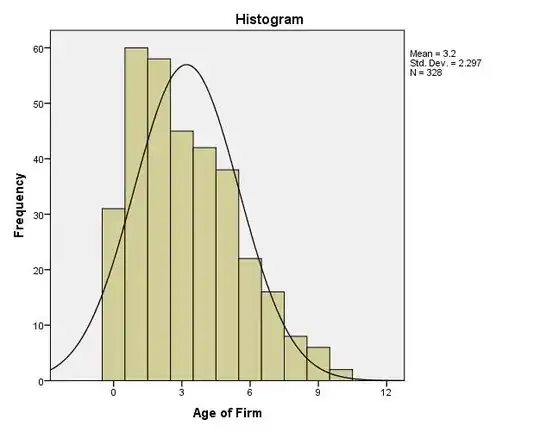
Histogram of age in cluster 1
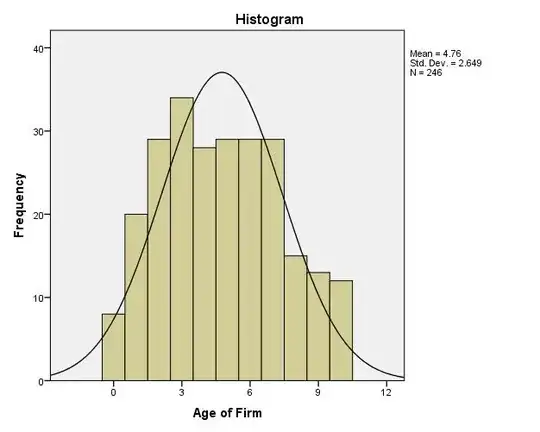
Histogram of Age in Cluster 2
Box plot of Age in Cluster 1
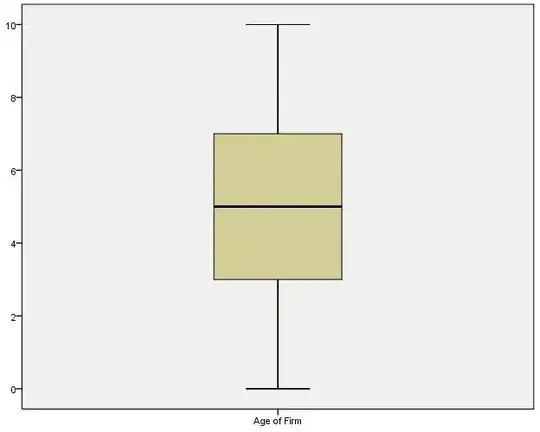
Box Plot of Age in Cluster 2
It has been suggested to use the Mann-Whitney test in this case, given that the assumption of normality is "not met".
- Does Mann Whitney work fine with continuous data? This link seems to suggest it does. Would SPSS automatically convert these into ranks?
- Zimmerman argues that t-test should work fine because it is scarcely affected by non-normality of the population!
- Sheskin (2007) suggests using a t-test anyway but using a more conservative approach (e.g critical values of t(0.01) instead of t(0.05).
How can I resolve this problem?