3

I have a problem which I am trying to fit into a classical regression/learning framework.

I have a dataset $D$ where each instance $d_i$ is a set of $(x,y)$ pairs, where $x$ is a non-negative number representing a position and $y$ is a non-negative value. For example, one $d_i$ could look like this:

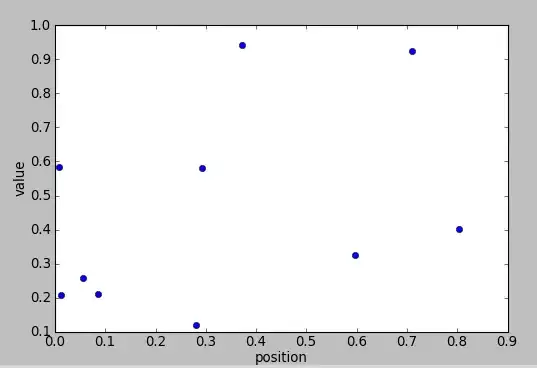
data instance

Given a vector of non-negative numbers $p$, I want to find a function $f$ which maps each $d_i$ to $p_i$ as well as possible, e.g. using least-squares minimizes $(f(d_i)-p_i)^2$. For example, such a function could be taking the the average of the $x$ values weighted by $y$, i.e. $f(d_i)=\frac{1}{\sum{y_j}}\sum{y_j*x_j}$. In general, the function will have some parameters, which I want to fit. For example, in the above example I could decide to use only the $k$ highest $y_j$ values, and I want to find the best $k$.

There are two straightforward ways to put this into a classical regression framework:

  1. Define $d_i$ as a vector of $y$ values, where the coordinate in the vector encodes the position $x$. This will be a problem since the $d_i$ vectors will be very sparse and at a given position most $d_i$ vectors will tend to have missing values.
  2. Define $d_i$ as a vector of $(x_i,y_i)$ pairs (e.g. one could "flatten" this to make it a 1d vector). The problem is then that I am artificially introducing coordinates, and so a general regression function might use the coordinates. This is a bad thing since the pairs are unordered so I expect $f(d_i)$ to be the same regardless of the order of the $(x,y)$ pairs.

I think this problem may be equivalent to this question: Learning from unordered tuples?, but I am not quite sure it is exactly the same - am I overlooking some natural ordered representation?

Community
  • 1
Bitwise
  • 6,379
  • 2
  • 22
  • 27

1 Answers1

1

The issues you point out are correct. Moreover, if one tries to artificially impose a total ordering on $\mathbb{R}^2$ (or more generally $\mathbb{R}^n$ with $n\geq 2$) then it would be unstable with respect to perturbations (this is because the Euclidean topology is not orderable for $n\geq2$).

For example, if $\mathbb{R}^2$ was lexicographically ordered we'd have $(1,0)<(1,200)$ but $(1,0)>(1-\epsilon,200)$ for any $\epsilon>0$.

The paper Deep Sets provides a few ways to achieve what you are looking for in a deep learning framework. I'll assume the labels $p_i\in\mathbb R$ for now. One idea is to express your desired function as

$$ f(d_i) = \rho\left( \sum_{(x,y)\in d_i} \phi(x,y) \right) $$

where $\rho$ and $\phi$ are suitable real-valued functions. This is manifestly permutation invariant and well-defined for sets of arbitrary finite cardinality. Since neural networks are universal approximators we choose to have $\rho$ and $\phi$ to be (deep) neural networks. Let $\theta$ represent the combined parameters of $\rho$ and $\phi$. The game is now to minimize the mean-square-error $\frac{1}{N}\sum_{i=1}^N(f(d_i)-p_i)^2$ by adjusting $\theta$ via backpropagation.

Edit: PointNet is another neural network architecture that can learn over point clouds (mainly used for $\mathbb{R}^3$). For your problem you may need to make modifications, but the main trick (in your setup) is to create the features by computing max's over your set with respect to some function $h$ and then feeding those $m$ features into some function $g$. This can be written as,

$$ f(d_i) = g\left( \max_{(x,y)\in d_i} h(x,y) \right) $$

where $g:\mathbb{R}^m\to \mathbb{R}$, $h:\mathbb{R}^2\to\mathbb{R}^m$ and the max is taken component-wise.

Once again, this is clearly permutation-invariant. As in Deep Sets, we would model the functions $g$ and $h$ as neural networks and then use backpropagation to minimize $\frac{1}{N}\sum_i (f(d_i)-p_i)^2$.

Christian Bueno
  • 443
  • 3
  • 9