I am interested in the modeling of binary response data in paired observations. We aim to make inference about the effectiveness of a pre-post intervention in a group, potentially adjusting for several covariates and determining whether there is effect modification by a group that received particularly different training as part of an intervention.
Given data of the following form:
id phase resp
1 pre 1
1 post 0
2 pre 0
2 post 0
3 pre 1
3 post 0
And a $2 \times 2$ contingency table of paired response information:
\begin{array}{cc|cc} & & \mbox{Pre} & \\ & & \mbox{Correct} & \mbox{Incorrect} \\ \hline \mbox{Post} & \mbox{Correct} & a & b&\\ & \mbox{Incorrect} & c& d&\\ \end{array}
We're interested in the test of hypothesis: $\mathcal{H}_0: \theta_c = 1$.
McNemar's Test gives: $Q = \frac{(b-c)^2}{b+c} \sim \chi^2_1$ under $\mathcal{H}_0$ (asymptotically). This is intuitive because, under the null, we would expect an equal proportion of the discordant pairs ($b$ and $c$) to be favoring a positive effect ($b$) or a negative effect ($c$). With the probability of positive case definition defined $p =\frac{b}{b+c}$ and $n=b+c$. The odds of observing a positive discordant pair is $\frac{p}{1-p}=\frac{b}{c}$.
On the other hand, conditional logistic regression uses a different approach to test the same hypothesis, by maximizing the conditional likelihood:
$$\mathcal{L}(X ; \beta) = \prod_{j=1}^n \frac{\exp(\beta X_{j,2})}{\exp(\beta X_{j,1}) + \exp(\beta X_{j,2})}$$
where $\exp(\beta) = \theta_c$.
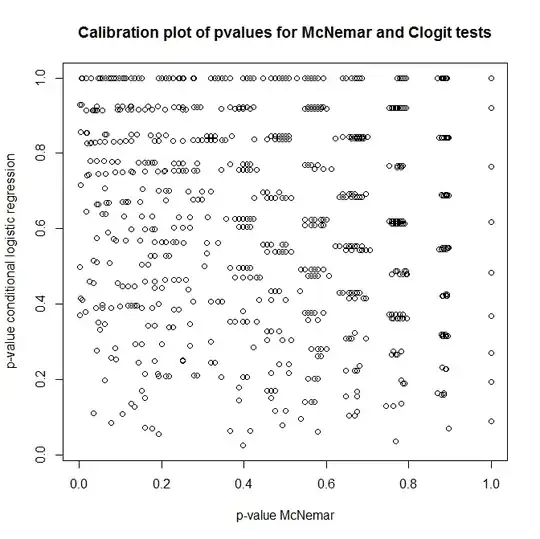
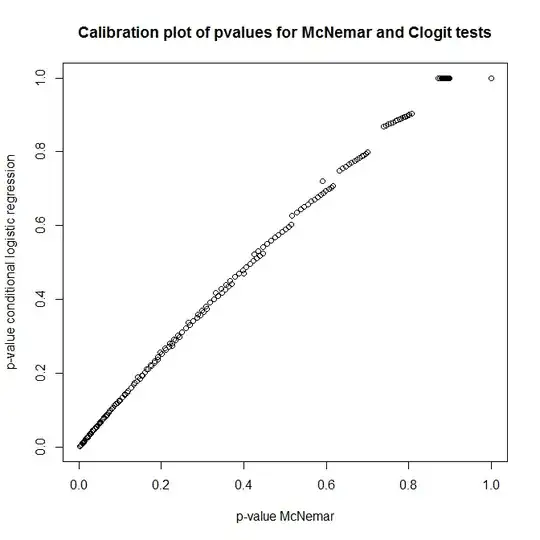
So, what's the relationship between these tests? How can one do a simple test of the contingency table presented earlier? Looking at calibration of p-values from clogit and McNemar's approaches under the null, you'd think they were completely unrelated!
library(survival)
n <- 100
do.one <- function(n) {
id <- rep(1:n, each=2)
ph <- rep(0:1, times=n)
rs <- rbinom(n*2, 1, 0.5)
c(
'pclogit' = coef(summary(clogit(rs ~ ph + strata(id))))[5],
'pmctest' = mcnemar.test(table(ph,rs))$p.value
)
}
out <- replicate(1000, do.one(n))
plot(t(out), main='Calibration plot of pvalues for McNemar and Clogit tests',
xlab='p-value McNemar', ylab='p-value conditional logistic regression')