Exercise 3.1.3 : Suppose we have a universal set U of n elements, and we choose two subsets S and T at random, each with m of the n elements.
What is the expected value of the Jaccard similarity of S and T ?
I am reading the book http://infolab.stanford.edu/~ullman/mmds/ch3.pdf
The above answer assumes that an element in $T$ may be repeated several times in $S$ (i.e. $S$ and $T$ are not sets but multisets); else the probability will not be $m/n$ uniformly.
I expect the answer should be more along the following lines:-
Let the number of common elements between $S$ and $T$ be $k$. Then, as mentioned by ack_inc in the comment to his answer, Jaccard similarity $Sim(S,T)=k/(2m-k)$.
Now, $Pr(Sim(S,T)=k/(2m-k))$ will be $\dfrac{{m\choose {k}} {n-m\choose m-k}}{n\choose m}$ since there are $n$ total elements, of which $m$ are in $S$ and $k$ are common. So the number of ways we can choose $m$ elements for $T$ is given by ${m \choose k}$ (choosing the $k$ common elements from $S$) times ${n-m\choose m-k}$ (choosing remaining $m-k$ elements).
Thus, $E(Sim(S,T))=\sum_{k=0}^{m} \dfrac{k}{2m-k} \dfrac{{m\choose {k}} {n-m\choose m-k}}{n\choose m}$.
However, simplifying the above expression is beyond my limited knowledge of combinatorial identities. If anyone can do so, kindly update the answer.
I'm posting an alternative solution.
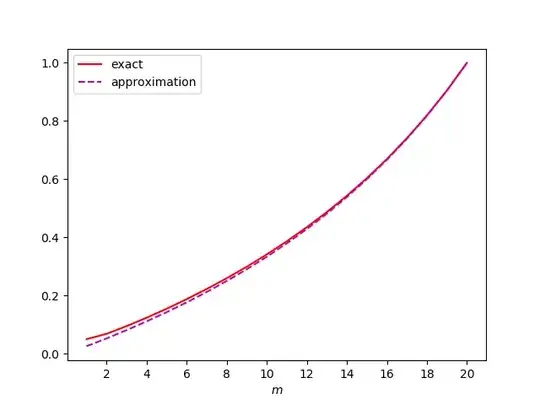
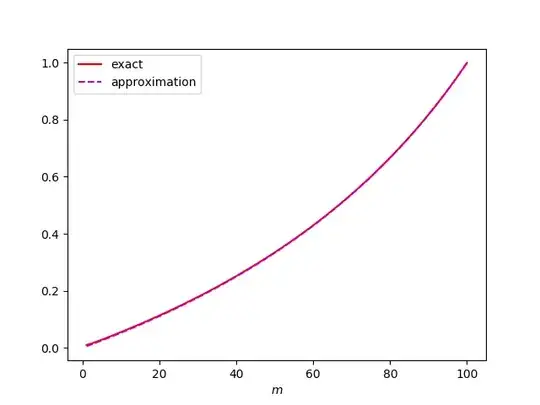
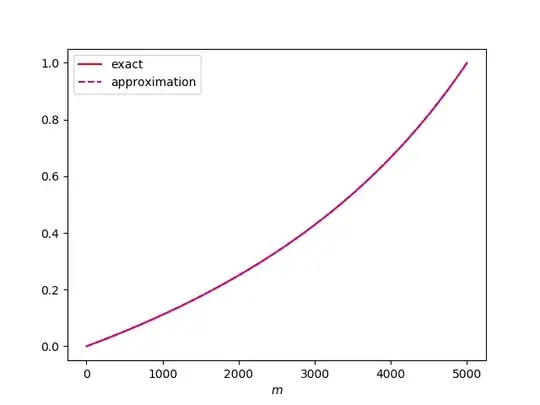
Jaccard similarity of two sets $S$ and $T$ is defined as the fraction of elements these two sets have in common, i.e. $\text{sim}(S,T)=|S\cap T|/|S\cup T|$. Suppose we chose $m$-element subsets $S$ and $T$ uniformly at random from an $n$-element set. What is the expected Jaccard similarity of these two sets? Suppose the $|S\cap T|=k$ for some $0\le k\le m$. Notice that for the first set, $S$, we have $\binom{n}{m}$ choices, while for $T$ we have $\binom{m}{k}\binom{n-m}{m-k}$ choices, because $k$ elements must be from $S$ and $m-k$ elements must not be from $S$. This gives us $$\Pr[|S\cap T|=k]=\frac{\binom{m}{k}\binom{n-m}{m-k}}{\binom{n}{m}},$$ meaning that $$\text{E}[\text{sim}(S,T)]=\sum_{k=0}^m\frac{\binom{m}{k}\binom{n-m}{m-k}}{\binom{n}{m}}\frac{k}{2m-k}.$$ Even though $\text{E}[|S\cap T|/|S\cup T|]\neq\text{E}[|S\cap T|]/\text{E}[|S\cup T|]=m/(2n-m)$, this expression seems to give good approximation.
Thanks to Mitja Trampus for pointing out an alternate solution, with $$\Pr[|S\cap T|=k]=\binom{m}{k}\frac{\binom{m}{k}}{\binom{n}{k}}\frac{\binom{n-m}{m-k}}{\binom{n}{m}},$$ giving the following expression: $$\text{E}[\text{sim}(S,T)]=\sum_{k=0}^m\binom{m}{k}\frac{\binom{m}{k}}{\binom{n}{k}}\frac{\binom{n-m}{m-k}}{\binom{n}{m}}\frac{k}{2m-k}.$$
(The above expressions are, of course, equivalent.)
EDIT: Regarding the simplification, perhaps applying the following identity (from Aigner's book, page 13) could work: $$\binom{n}{m}\binom{m}{k}=\binom{n}{k}\binom{n-k}{m-k}.$$
Each item in T has an $\frac{m}{n}$ chance of also being in S. The expected number of items common to S & T is therefore $\frac{m^2}{n}$.
Exp. $\text{Jaccard Similarity} = \dfrac{\text{No. of common items}}{\text{Size of T} + \text{Size of S} - \text{Number of common items}} = \dfrac{m}{2n - m}$ (after simplification.)
I agree with blazs answer - just want to add a small correction (credit to another guy in the course who pointed it out).
The summation does not start at 0. (you'll see it if you make n=100 and m=99)
$$ \text{E}[\text{sim}(S,T)]=\sum_{k=max(0, 2m-n)}^m\binom{m}{k}\frac{\binom{m}{k}}{\binom{n}{k}}\frac{\binom{n-m}{m-k}}{\binom{n}{m}}\frac{k}{2m-k}. $$
I just want to add the following:
As pointed out, ack_inc's answer is not correct and can serve only as an approximation. Also, the lower bound should be $\max\{0, 2m - n\}$ instead of $0$, as GM1313 mentions.
I needed to compute the similarities for $1\leq m\leq n$ where $n = 5000$ or even bigger, so computing all the probabilities $P_{n, m}[|S\cap T| = k]$ (blindly following the definition)
Therefore, I used the fact that ${a \choose b + 1} = \frac{a - b}{b + 1}{a \choose b}$ to speed up the process, and compute the probabilities recursively, starting with the biggest one.
I also used the approximation $m / (2n - m)$ and actually, it is really good, especially for larger values of $n$ (curves for $n\in\{20, 100, 5000\}$):
