Determining values of correction factor based on x bins in observed vs. actual data

Question

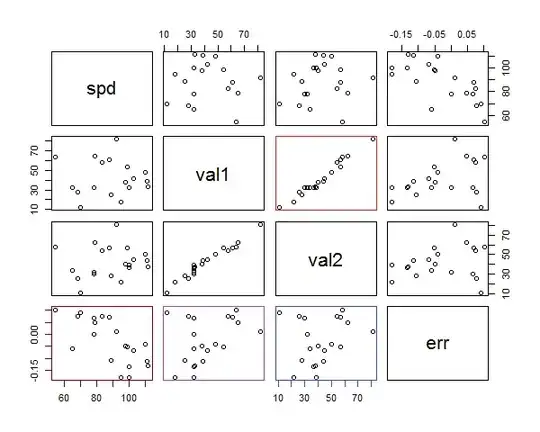
I am trying to automate a problem I usually solve by hand.

I have a sensor that collects data from the field. Every 6 months or so, I have to do a calibration on that sensor by collecting x data points. Using a calibrated device, I measure the same data measured by the field sensor and I have the following table:

    Field  | Actual 
#   spd val val   err
1    89 25  28  -10.71%
2   100 32  39  -17.95%
3    54 64  58   10.34%
4    65 32  34   -5.88%
5    70 12  11    9.09%
6   100 32  37  -13.51%
7   110 48  50   -4.00%
8    78 32  32    0.00%
9    95 18  22  -18.18%
10   92 82  81    1.23%
11   78 32  30    6.67%
12   98 38  40   -5.00%
13  103 42  45   -6.67%
14   99 54  57   -5.26%
15   88 61  57    7.02%
16   79 65  62    4.84%
17   83 58  54    7.41%
18  111 39  44  -11.36%
19  112 33  38  -13.16%
20   68 28  26    7.69%

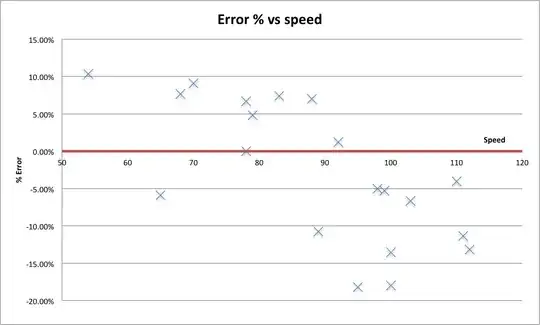
The following is the Error versus Speed plot:

How I currently solve this problem:

• look at the data visually and determine how the data is "trending".
• I can split the data in x bins (depending on how new the sensor is, newer sensors can divide in to multiple bins)
• For the example above, I notice 3 bins:
  • 50 to 70 - around 10% with one outlier
  • 70 to 95 - around 3-4% with one outlier
  • 95 to 120 - around -10% with one outlier.
• I then create the three bins for the sensor
• based on these bins, I determine a fudge or correction factor for each bin
• I then retest the sensor for more counts and redraw the graph. and repeat the process
• this process is time consuming especially when I have 10 sensors to look after, and that process can take up to 3 hours to complete

Question:

How can I create a statistical or mathematical solution to aid me in solving my problem?

Edit 1:

Some clarification:

• Speed: speed as the object hits the sensor
• Value: read by the sensor
• Final result is to obtain an average error of less than 6% on all reads
• Sometimes I collect more than 20 reads
• I would like to have uniformly calibrated across all ranges of speed as in the difference between actual vs measured to be relatively consistent so that every measured value could be used without significant error

Edit 2:

• tools I have access to are Excel, Python, and R (in that order of usability for myself)

Edit 3:

• Each object that's hitting the sensor is different in shape, size, and speed, so therefore the object hitting at any speed is not related to the size of the object. The sensor as it gets older tends to reads values differently at different speed bins.

Edit 4:

• Based on @Glen_b 's answer, I created the following MS Excel file for non binned results: http://97.107.136.148/results_stats_se.xls . Disregard the steer columns in the excel sheet. as it does not impact this problem.

Edit 5:

• I collected more data as shown below.
• Sub is a partial measurement of the object, so sub is part of the full_measurement.
• There is no ratio relationship between sub and full other than it's sub

Data:

Speed    Non Calibrated sensor        Calibrated sensor    
Speed    Sub_1 Measurement_full    Sub_1    Measurement_full
sensor 1
  88     5500      51800            5610    49010
  95     5400      66000            5630    62700
sensor 2
  99     4700      34600           43100    35850
 103     5400      38200            5160    35360
  84     4900      47700            4550    48330
 101     5400      44800            5190    43050
 106     5200      28400            5290    24390
  96     4900      44900            4730    42900
 104     5300      35000            5350    35290
 102     5400      47700            5290    46810
  99     5500      35500            5270    34410
  89     5400      35600            5290    35490
  98     5300      39300            5240    37580
sensor 3
  93     5000      35600            4860    31050
  79     5500      41000            5130    37810
  92     4600      30700            4750    29720
  99     4900      47100            4820    46230
  94     5100      48300            4990    48230
  93     5300      51600            5460    54850
  99     5100      41700            4910    38960
  85     5100      42200            4960    42810
  81     5500      44100            5120    37960
  98     5600      64300            5550    62510
 102     5300      33400            5380    31220
sensor 4
 106     4800      35000            4430    30440
  99     5900      56300            5590    52740
  78     5900      56300            5730    54380
  96     6300      49100            5620    47790
  98     5500      42100            5340    38340
  70     5300      45700            4750    43670
  77     5100      37900            5100    34470
 106     4300      12100            3930     9750
 107     5800      35600            5270    28930
  90     3800      32300            3310    29390
  75     5800      62200            5490    61470
  88     4900      39200            5010    35720
sensor 5
 104     4500      44200            5000    45120
  95     5460      49400            5440    48520
 104     4700      33900            5210    33420
  86     5200      36400            5280    35140
  88     5000      49500            5760    52250
  94     5300      44400            5200    43310
  95     5200      54000            5370    54460
  99     5100      37000            5410    35600
  91     5600      62400            5540    61860
  95     5400      38000            5310    32510
  94     5100      49300            4990    46210
 101     4800      44300            5380    45130
 100     6600      23700            7500    24630
 105     5100      29200            5400    26740
  94     5500      42400            5730    40760
  89     5200      49600            5270    49570
  99     5300      47100            5700    47970
 100     4900      36600            5220    36790
  90     7200      25500            7340    23480
 100     5200      36500            5410    36210

Answer 1

It looks to me like it might potentially make sense to account for the way the error changes with the second (calibrated) val as well as with speed. If you're only interested in the relationship with speed, it looks like linear regression would be a good first suggestion.

First, let's look at your data; this is every variable against every other variable, usually called either a scatterplot matrix or a pairs plot:

Features in the pairs plot:

The plot of err vs spd, bottom left, outlined in reddish brown. This is the same plot you show and indicates a clear downward trend. This is what prompts me to suggest linear regression of some kind as a 'first attempt'.

Consider the plot of val1 against val2 (val2 is the calibrated-instrument measurement, the one you want your field measured-val to be close to), the plot near the middle, outlined in red. It has a nice straight-looking relationship, as you'd hope. There's a 'flat' part where a whole bunch of different calibrated values near 32 were recorded as '32'; this potentially suggests some kind of issue with the device (though it could also be mere chance combined with the rounding that's there).

Consider the err vs val2, the plot in blue. Values to the left of $\text{val2}\leq 32$ (roughly) look very noisy there and then there's less noise but a distinct upward trend after that. You can see a similar effect in the plot of err vs val1 (the purple-outlined plot in the last row; this is potentially useful, because val2 isn't available normally).

Edit: there's also a suggestion of nonlinearity in the relationship of the two 'val' variables with spd (unsurprisingly).

---

Linear regression (first model):

This fits a straight line. You could just fit a straight line of err against spd, but this misses a bunch of potential value in the information you have in the other variables.

The usual form of linear regression is via least squares, and this is probably easiest to do, but given the possibility of outliers you mention, you may want to consider a more robust alternative.

Here's a linear regression done in R. Note that my err variable isn't multiplied by 100, so if you did it with your numbers, your coefficient would be 100 times as big:

 mdl1 <- lm(err~spd,calib)
 summary(mdl1)

Call:
lm(formula = err ~ spd, data = calib)

Residuals:
     Min       1Q   Median       3Q      Max 
-0.12761 -0.02540  0.01683  0.04742  0.09650 

Coefficients:
              Estimate Std. Error t value Pr(>|t|)    
(Intercept)  0.3242267  0.0865953   3.744 0.001485 ** 
spd         -0.0039833  0.0009619  -4.141 0.000613 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 0.06867 on 18 degrees of freedom
Multiple R-squared:  0.4879,    Adjusted R-squared:  0.4594 
F-statistic: 17.15 on 1 and 18 DF,  p-value: 0.0006134

The residual standard error, 0.0687 suggests that the typical error (let alone the maximum error!), even after adjustment is still a good deal larger than you'd like.

Looking at the diagnostics, the model doesn't look too bad. There are low outliers, and the variation looks bigger near the middle, with a decrease at larger fitted values.

---

The relationship between val2 and val1

Before we plow on with that, though, we should investigate the relationship between the field measured val and the calibrated one. The pairs plot above doesn't make it obvious, but I could discern a slight bend... and given the pattern in the err vs val2 plot, I decided to take a closer look:

Clearly there's a 'bend' here! You shouldn't ignore that; it's a source of a fair amount of your error.

It's clearer still if you look at the raw error:

Edit: This effect remains if you remove the clump of values at 32 --

The problem is, of course that in the field you don't know val2 and you need val1 to estimate the 'gold standard' value -- yet val1 is the 'noisy' measurement. This is sometimes called an 'inverse regression' problem.

It's probably worth your time to google on this; or rather on one of these:

inverse regression -sliced --- (because this avoids some not-so-relevant hits)

inverse regression calibration

Your problem is a calibration problem (you're trying to figure out how to estimate val2, the 'accurate' measure, from val1, the noisy one), but you have the advantage of a second predictor, which seems to add useful information to the raw calibration curve.

---

A second, simple regression model

With the decrease in variability against fitted in the first model, and the fact that the actual problem is to try to 'back out' val2 from this, consider modelling the actual error rather than the percentage error.

Further, while this model will ignore that 'bend' in the data, it will consider val2 in the model for val1. Well, we will fit two models in order to see if there's value in extending it:

summary(m1)

Call:
lm(formula = I(val1 - val2) ~ spd, data = calib)

Residuals:
    Min      1Q  Median      3Q     Max 
-4.8978 -1.3288 -0.3747  1.5850  4.8034 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 13.35791    3.22609   4.141 0.000614 ***
spd         -0.16092    0.03583  -4.491 0.000283 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 2.558 on 18 degrees of freedom
Multiple R-squared:  0.5284,    Adjusted R-squared:  0.5022 
F-statistic: 20.17 on 1 and 18 DF,  p-value: 0.0002827

We can't really compare this model with the previous one, it's not on the same scale (however, we again see that spd is needed to 'adjust'). Now lets add val2:

summary(m2)

Call:
lm(formula = I(val1 - val2) ~ spd + val2, data = calib)

Residuals:
    Min      1Q  Median      3Q     Max 
-4.4331 -0.8054  0.0845  1.0342  3.4050 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 10.55003    2.77761   3.798  0.00144 ** 
spd         -0.17419    0.02954  -5.897 1.76e-05 ***
val2         0.09427    0.02976   3.168  0.00562 ** 
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 2.088 on 17 degrees of freedom
Multiple R-squared:  0.7034,    Adjusted R-squared:  0.6686 
F-statistic: 20.16 on 2 and 17 DF,  p-value: 3.258e-05

We see that the largest and smallest residuals are smaller and that spd has a very similar effect to before. The residual standard error is about 20% smaller and the val2 effect is significant. That is, if we want to try to 'guess' val2 from spd and the noisy val1, we should not ignore the linear relationship between val1 and val2. The diagnostics (not shown) are better, though the presence of low outliers does suggest that a more robust method might get a little closer for the bulk of the data.

If you do this with the relative error instead, you don't see as much value in adding val2, but I'd still include it (and the model diagnostics aren't nearly as nice, because the size of the error really isn't constant on the percentage scale; it's much nearer to constant on the scale of actual error).

It doesn't get you down to 6% error, but that's mostly because the percentage errors for the low vals are always going to be large on the percentage scale, even though they're nice looked at as raw errors), but if you want to lower it further, you'll need more data in order to estimate a calibration curve (and your job will become more complex) - there's a suggestion of curvature with both val2 and spd; I'd probably look at natural spline regression if you went that direction.

---

Using Excel:

The linear regressions can be done in Excel, but some of the diagnostics won't be available, and if come to trying to calibrate a curve, it becomes very unwieldy. I think it's worth putting the data into R and learning the tools.

---

Some issues with sample splitting:

Take a look at some of the discussion here. In the links there, it's discussing the idea of splitting samples into either three or two groups instead of fitting a line, where the actual relationship is smooth (doesn't seem to have 'jumps'). If some of the terms aren't clear in the links, please ask.

Justification for low/high or tertiary splits in ANOVA

(However, if your example data is typical, you may actually have jumps. In that case, you might want to consider models that pick up such jumps without requiring you to identify them by hand - and you would want to account for the potential overfitting as well)