Interpreting matrices of SVD in practical applications

Question

I have a question regarding the interpretation of the different matrices produced by singular value decomposition.

Suppose a mxn matrix $A$ containing n images of m pixels. So each column of this matrix when reshaped is an image. The images are actually wavelets transformations but that bears no relevance to the question. Furthermore, the first k columns of $A$ are images of dogs and the remaining columns are images of cats. So I have something like this:

wavelet_dc = np.hstack((wavelet_dogs, wavelet_cats))
U, S, V = svd(wavelet_dc, full_matrices=False)

What is the interpretation for U, S and V? I know we can build the original image based on a sum such as $A = \sum_{i} u_{i}s_{i}v^{T}_{i}$ in which $u_{i}$ and $v_{i}$ are column vectors of U and V, respectively. I also know that $S$ determines the most important modes of the original matrix and that the columns of U are the features associated to those modes. However, what role does V play in this matrix? I'd like to know how to think about V in practical applications (that is, more than as a rotation in the geometric interpretation of SVD)

Furthermore, suppose I plot V in the following way:

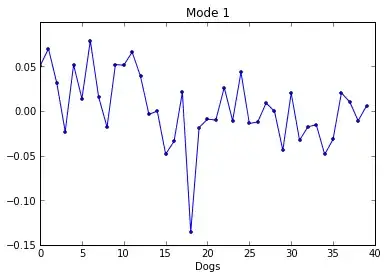
plot(V[0:40, 0], 'o-', markersize=3)

Since V is a nxn matrix, I don't know how to interpret it, but I think this code is actually taking the first 40 rows and the first column of V. As I understand V as:

$$V = \begin{pmatrix}v_{1}^{T} \\v_{2}^{T} \\\vdots \\v_{n}^{T}\end{pmatrix}$$

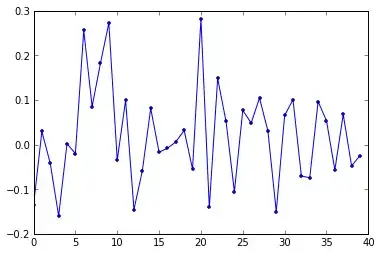
I think the plot is referring to the first component of the 40 vectors $v_{1} ... v_{40}$ but what does it mean? In the Coursera class "Computational Methods for Data Analysis", this is described as the dogs for the first mode and V[0:40, 1] would be the dogs for the second mode, and so on. You can see the notes here, figure 159, page 388. This is assuming of course, that at least the first 40 columns of $A$ contained images of dogs. In the class, they also plot V[80:120, 0] because their matrix $A$ actually has the first 80 columns representing images of dogs and the last 80 columns representing images of cats, so V[80:120, 0] is plotting the first 40 images of cats.

UPDATE:

According to the video lectures, W8_L21_P3-Features: https://class.coursera.org/compmethods-002/lecture/76, they seem to interpret V[0:40, x] as the projection of the first 40 dogs onto the modes. Well, V has dimensions nxn which is the number of images, however, I wouldn't interpret it as "dogs". In any case, I think such projections shouldn't be V[0:40, 0] but V[0, 0:40] because these are the first 40 components of the vector $v_{1}^{T}$ that multiplies the first mode $s_{0}$. However, please let me know if I made a mistake.

Answer 1

I think I have an answer. If you notice a mistake, let me know.

One interpretation explained in the book suggested by Cam.Davidson.Pilon is the factor interpretation. This tells you that a matrix $A$ with n rows and m columns can be decomposed into a matrix $C$ with $n$ rows and $r$ columns, a matrix $W$ with r rows and r columns and a matrix $F$ with $r$ rows and $m$ columns. So suppose that your matrix $A$ contains $n$ objects and m attributes. As a consequence of this decomposition, you can think of $C$ as a different view of the $n$ objects, except that instead of using $m$ pieces of information, you use r pieces of information (usually, $r < n$). Similarly, $F$ can be thought as a different view of the attributes of $A$, again using $r$ pieces instead of $n$.

This description applies to general decomposition. The difference in SVD is that the matrices $W$ and $F$ have $r=n$, but the same interpretation is possible.

Therefore, in the example I described in the question, the matrix $A$ looks like this:

$$ A = \begin{pmatrix} a_{1,1} & a_{1,2} & \cdots & a_{1,n} \\\ a_{2,1} & a_{2,2} & \cdots & a_{2,n} \\\ \vdots & \vdots & \ddots & \vdots \\\ a_{m,1} & a_{m,2} & \cdots & a_{m,n} \end{pmatrix} $$

in which the rows are attributes (in this case, pixels) and the columns are objects (dogs and cats). An SVD decomposition of this matrix would like this:

$$ A = U\Sigma V^{*} $$ $$ A = \begin{pmatrix} u_{1,1} & u_{1,2} & \cdots & u_{1,n} \\\ u_{2,1} & u_{2,2} & \cdots & u_{2,n} \\\ \vdots & \vdots & \ddots & \vdots \\\ u_{m,1} & u_{m,2} & \cdots & u_{m,n} \end{pmatrix} \begin{pmatrix} \sigma_{1} & 0 & \cdots & 0 \\\ 0 & \sigma_{2} & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\\ 0 & 0 & \cdots & \sigma_{n} \end{pmatrix} \begin{pmatrix} v_{1,1} & v_{1,2} & \cdots & v_{1,n} \\\ v_{2,1} & v_{2,2} & \cdots & v_{2,n} \\\ \vdots & \vdots & \ddots & \vdots \\\ v_{n,1} & v_{n,2} & \cdots & v_{n,n} \end{pmatrix} $$

Following this factor interpretation, every row of $V^{*}$ corresponds to a factor, the first columns correspond to dogs and the last ones to cats. So, let's take the first 40 columns of $V^{*}$ of the first factor. This should be:

fig = figure()
ax = fig.add_subplot(1,1,1)
ax.plot(V[0, 0:40], 'o-', markersize=3)
ax.set_xlabel('Dogs')
ax.set_title('Mode 1')

This plot describes the value of the first factor for the first 40 dogs. Since these values $v_{1,1}, ... v_{1,n}$ are going to be multiplied by $\sigma_{1}$, they are associated to the first mode:

$$\Sigma V^{*} = \begin{pmatrix} \sigma_{1} v_{1,1} & \sigma_{1}v_{1,2} & \cdots & \sigma_{n} v_{1,n} \\\ \sigma_{2} v_{2,1} & \sigma_{2}v_{2,2} & \cdots & \sigma_{2}v_{2,n} \\\ \vdots & \vdots & \ddots & \vdots \\\ \sigma_{n}v_{n,1} & \sigma_{n}v_{n,2} & \cdots & \sigma_{n}v_{n,n} \end{pmatrix}$$

Likewise, V[0, 40:80] produces the first factor for the first 40 cats.

Don't read too much into the values because I used a low quality dataset just to reproduce this part of the course.