Mboxcox in Stata suggests transforming my variables using a power of 0.1 for the independent variable, and 0.4 for the dependent variable.
I have run the model, and it fixes problems associated with the assumptions of OLS. But certainly, it complicates matters in terms of interpretations.
Please outline possible interpretations and solutions.
Dependent variable is in millions of dollars, and independent variables are number of years. and a number of dummies which do not require transformation.
In my experience, likelihood methods for finding Box-Cox transformations of data are both poor (in performance) and unstable. They are contrary to the spirit and intended use of transformations, too, which include:
Finding interpretable re-expressions of data,
Attempting to linearize relationships,
Attempting to achieve homoscedastic relationships,
Allowing interactive exploration of data analysis options,
Using calculations that are resistant to outlying values, and
Being robust to alternative (but plausible) assumptions about data behavior.
Instead, by its very nature, a likelihood-based method (such as mboxcox, which aims to achieve [approximate] multinormality), violates all these aims, as you can check, one-by-one.
Nevertheless, almost since the time Box-Cox transformations were first described, people have been coming up with automated ways to estimate them. Few work well, but many sometimes give an approximate starting point, or range of starting points, to streamline the exploration.
Before we go on, let's establish the correct use of mboxcox. A careful reading of the article on which this code is based find this important suggestion: "Following the advice of Sheather (2009), we round the suggested powers to the closest interpretable fractions" (emphasis added). Traditionally, an "interpretable fraction" [sic] is a value that might appear in a physical theory: $1/2$, $1/3$ (and their negatives) along with whole values $0, 1, 2$ (and their negatives). Thus it was never intended that the user accept the output of mboxcox as-is: it has to be rounded according to knowledge of the data and the objectives of the analysis.
As a quick test of mboxcox, I applied it to the classical Mercury vapor pressure dataset popularized by John Tukey. It is the simplest multivariate dataset possible, containing $19$ (temperature, pressure) pairs with extremely small errors, leading to little uncertainty in what the best Box-Cox parameters ought to be. An exploratory data analysis (EDA) of this dataset is described in my answer at Box-Cox like transformation for independent variables?. It finds, correctly, that (after converting temperature to absolute temperature) the Box-Cox powers should be $0$ for the pressure and $-1$ for the temperature. (In this case, unlike in most data analyses, there is a correct answer given by a well-known physical law. That is why it makes a fine proving ground for any automated procedure.)
By contrast, when we apply mboxcox, at first it complains that it cannot deal with the zero temperature. If we simply exclude it--it will later found to be an outlier, anyway--it reports that the Box-Cox parameter for pressure should be $0.3420578$ (comfortably close to the convenient $1/3$, with a $95$% CI from $0.22$ to $0.46$) and for temperature should be $2.2386$ (CI from $1.5$ to $3.0$), which could be taken as close to $2$. Good, right? Both are highly significant.
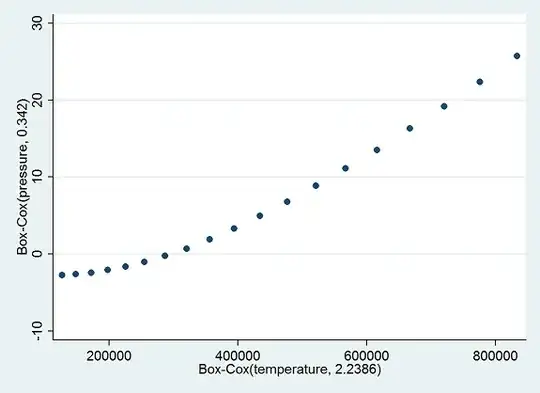
But, as we know--and can see in the nonlinear trend in the scatterplot--these are awful results, because we really need to be using the absolute temperature. Let's start over after adding $273$ degrees to the temperatures. Because there will no longer be a problem with zero, we will include all the data. This time mboxcox reports that the Box-Cox parameters should be $0.0712114$ for pressure and $0.2411739$ for temperature (CI from $-0.8$ to $1.3$). Even after rounding both values and accounting for the long confidence interval for temperature, the results are far from correct--even though the $R^2$ value in the resulting regression of (transformed) pressure on (transformed) temperature actually exceeds what is achieved when the correct parameters are used!
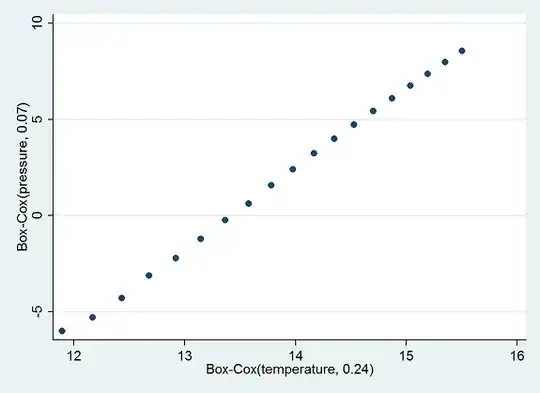
Although this is a beautifully linear relationship on this scale, examination of the residuals shows it leaves much to be desired.
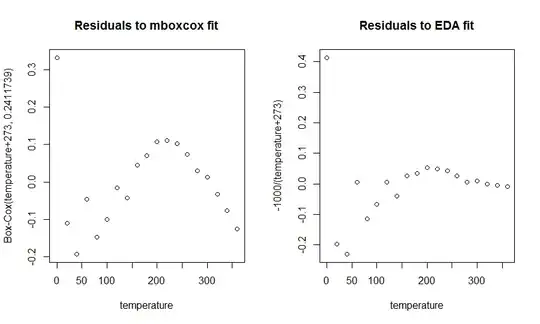
NB: The y-axes on these plots are not directly comparable, because they represent different re-expressions of the pressures. What is of concern are the apparent patterns of non-linear behavior and serial correlation in each plot. The right plot does a better job at identifying the outlier (at a temperature of 0) and is much more horizontal than the left plot (mboxcox), which shows a clear curvilinear trend and is nowhere horizontal.
If we remove the case with the lowest temperature (which is the main source of the difficulty, even though it's not much of an outlier), mboxcox finally gets it right: it estimates a parameter of $0.013$ for pressure, which clearly rounds to $0$, and $-0.8559$ for temperature (CI from $-1.4$ to $-0.3$), which anyone would round to $-1$, with a possible $-1/2$ contained in the confidence interval. But it took three tries and required an insight (the use of absolute temperatures) that dropped out of the original EDA but had to be supplied by the analyst using mboxcox.
With the results of this quick look we may deduce that mboxcox indeed has the potential to deliver useful starting points for an EDA of multivariate data, provided it is carefully protected by first identifying outliers, that the estimates are appropriately rounded, and that the data are further explored to make sure that other Box-Cox parameters (even those far from the "optimal" ones) might not serve better. I would give little weight or credence to the mboxcox results without extensive follow-on analysis, because although it aims at establishing an approximate multivariate normal distribution of the data, that does little to assure either linearity or homoscedasticity and likely places too much emphasis on transforming the independent variables instead of the dependent variable itself.
Although you have given some details, this is too close to "I have some data, want to fit a regression, and can't interpret my model easily" to allow much to be said easily that is likely to be really helpful. Too much depends on what your field is, what models make sense or are interesting substantively in that field, etc., not to mention finer details of your data. Not least, what is "interpretation"? It can mean anything from "I don't understand the statistics here, so need technical explanation on my level" to "What does this imply in subject-matter terms?".
But (personal opinions mixed in here)
If your response or dependent variable is a count, I would expect Poisson regression to make much more sense than regression. Even if it is a measured number of years that is zero upwards, I would still expect that. http://blog.stata.com/tag/poisson-regression/ is one account rich in Stata context.
The idea of Box-Cox is letting your data indicate which transformations make most sense. However, Box-Cox like much else is a knife that you can cut yourself with. The original examples are instructive: Box and Cox didn't use the precise powers indicated, but logarithm and reciprocal, which made sense on other grounds. Unless you are fitting a power law, it is usually more practical to regard Box-Cox as pointing to one of a small number of standard transformations, most commonly log, root or reciprocal. It is rare that (say) powers such as 0.4 can be related to substantive literature unless there is good theory underpinning the use of fractional powers in the first place. The fact that most common transformations can be regarded as members of a family doesn't mean that all members of that family are equally helpful.
