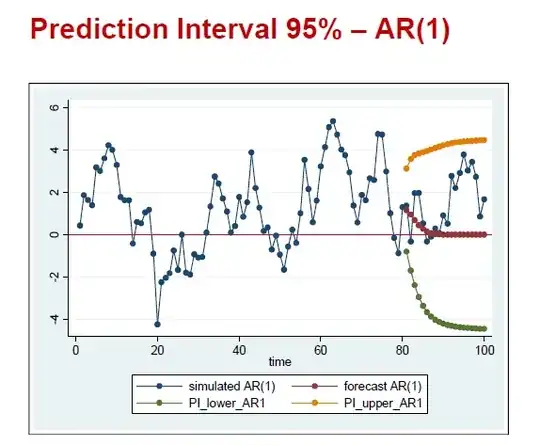
I've been told in my current textbook that for approximation of the exact distribution by means of $X^2$ or $G^2$ the expected frequencies have to be $\ge 5$.
The book says that the approximation could be biased, but I wonder how and why?
I've been told in my current textbook that for approximation of the exact distribution by means of $X^2$ or $G^2$ the expected frequencies have to be $\ge 5$.
The book says that the approximation could be biased, but I wonder how and why?
The counts are discrete. The chi-square approximation for $X^2$ relies on the counts being approximately normally distributed; when all the expectations are greater than 5 the chi-square approximation tends to be reasonable; it's a pretty arbitrary cut-off. For $G^2$ it relies on an asymptotic argument; I think it generally comes in more slowly than for $X^2$. The condition of all expecteds above 5 is very old; many more recent papers suggest somewhat less stringent requirements are fine for the Pearson.
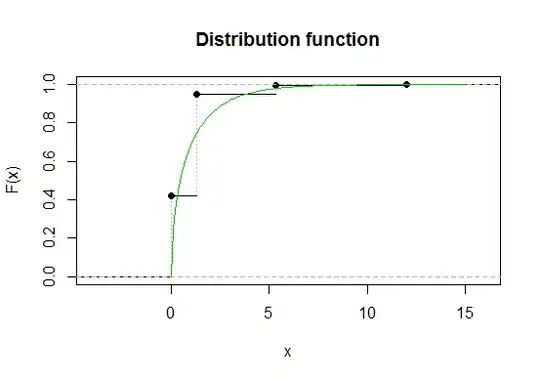
Basically, when a discrete r.v. has nearly all its probability concentrated in a few values, even the best of continuous approximations is not going to be much good. Consider a chi-square goodness of fit test for a bernoulli(.25), where we have 4 observations. The chi-square is the sum over the number of $0$'s and $1$'s of the usual $(O-E)^2/E$. The two expected counts are 3 and 1. The actual distribution of the chi-square statistic takes exactly four values. The chi-square(1) has a 5% critical value of 3.84, but the 95th percentile of the actual distribution is 5.33.