2

I used the MATLAB code written below to create the following probability density function. It creates the familiar hill-shaped distribution.

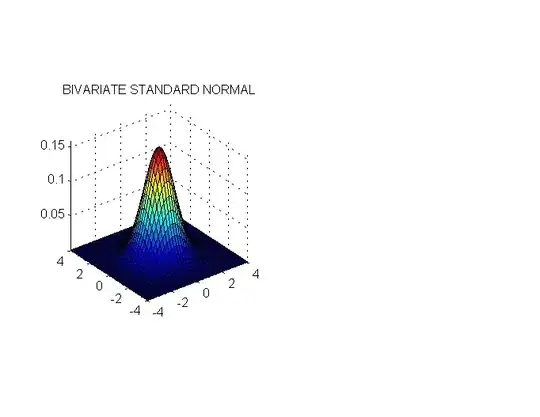
bivariate normal distribution

I'm interested to see (whether via MATLAB code or just an linked image) a PDF plot of a distribution that is univariate normal but is multivariate platykurtic or multivariate leptokurtic. Failing that, I would like to read a description of how my image would like different if it was univariate normal but is multivariate platykurtic or multivariate leptokurtic. At present I cannot visualize what that would look like.

MATLAB code:

function prob = csevalnorm(x,mu,cov_mat);
[n,d] = size(x);
% center the data points
x = x-ones(n,1)*mu;
a = (2*pi)^(d/2)*sqrt(det(cov_mat));
arg = diag(x*inv(cov_mat)*x');
prob = exp((-.5)*arg);
prob = prob/a;

% Get the mean and covariance.
mu = zeros(1,2);
cov_mat = eye(2);% Identity matrix
% Get the domain.
% Should range (-4,4) in both directions.
[x,y] = meshgrid(-4:.2:4,-4:.2:4);
% Reshape into the proper format for the function.
X = [x(:),y(:)];
Z = csevalnorm(X,mu,cov_mat);
% Now reshape the matrix for plotting.
z = reshape(Z,size(x));
subplot(1,2,1) % plot the surface
surf(x,y,z),axis square, axis tight
title('BIVARIATE STANDARD NORMAL')
user1205901 - Reinstate Monica
  • 11,303
  • 26
  • 77
  • 152
  • 2
    Good question, it is difficult to superimpose 3d (or 2.5d) data in a plot. Perhaps visualize the difference of the densities, or just make two small multiple plots of the different densities with the same perspective. In a 2d graph, I've seen cartographers superimpose contour lines and kde estimates (displayed via color), but they are difficult graphics to interpret for sure. – Andy W May 21 '13 at 13:43
  • 1
    Given that kurtosis usually refers to properties of the fourth moment and bivariate distributions have not one but *five* distinct fourth moments, could you more precisely explain what you mean by "platykurtic" or "leptokurtic" in the bivariate case? – whuber May 21 '13 at 14:26
  • I suspect I'm using the terms imprecisely. I'm seeking a picture of a bivariate distribution that has non-normal kurtosis and don't particularly mind in what way the kurtosis is non-normal. What has occurred is that I've run a test of multivariate kurtosis and a program has told me the results are non-normal. I'm attempting to picture what could potentially look like, or seeking an explanation of why attempting to picture this is impossible in principle. – user1205901 - Reinstate Monica May 21 '13 at 15:57
  • Perhaps you could give more detail about what it was that led to the question? That might make what you're asking about more clear. – Glen_b May 21 '13 at 23:09
  • 3
    See [this fantastic answer](http://stats.stackexchange.com/a/30205/6633) for a huge collection of bivariate nonnormal distributions that are marginally normal. – Dilip Sarwate May 22 '13 at 02:13
  • @Glen_b Someone asked me to show them a bivariate normal distribution so I showed them that MATLAB plot. Then they asked me to show them a bivariate non-normal distribution so I drew that on a piece of paper. Then they asked me to show them a bivariate non-normal but univariate normal distribution and I had no idea what to draw. – user1205901 - Reinstate Monica May 22 '13 at 02:58
  • @DilipSarwate Thanks very much for linking that, the heat maps are extremely close to what I was trying to plot. – user1205901 - Reinstate Monica May 22 '13 at 02:59

0 Answers0