4

I have a sample of 608 subjects and I need to remove outliers for age. In R, the boxplot appears like this:

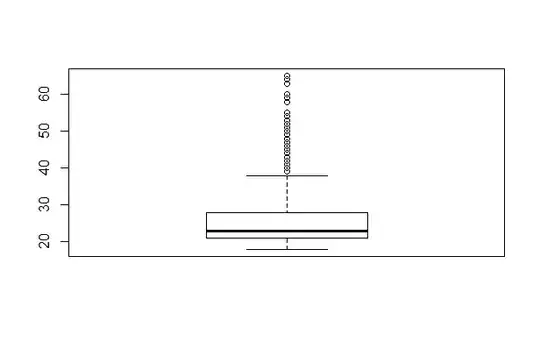
enter image description here

It shows 74 outliers:

> length(boxplot(mydata)$out)
[1] 74

After I have removed these outliers, should I take a new look at the boxplot with the new data? If I do that, the boxplot still contains other outliers:

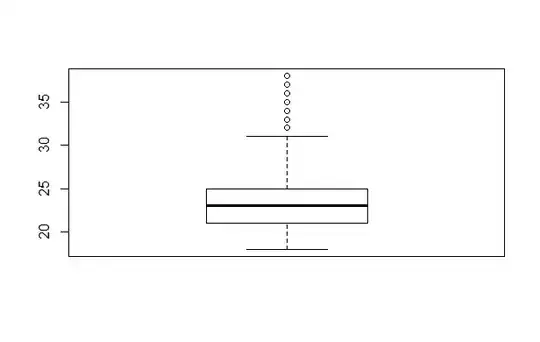
enter image description here

Questions:

1. Is this a problem?

2. Is this method appropriate for removing outliers for age?

EDIT: I will not use age as a variable in a regression model. I want just to remove outliers for age in order to obtain a more uniform sample (this is a students sample). For example, I have one subject 60 years old, while the mean age of my sample is 26.6. For this reason, I was also thinking to remove outliers not by boxplot but by ± 3 standard deviations from the mean. From my sample, I then will select two groups of subjects for further testing.

this.is.not.a.nick
  • 862
  • 2
  • 13
  • 25
  • Interesting. It would be even better if you could post a small random subsample (say 100 observations) of your data. You can do this with the dput() command in R. – user603 May 08 '13 at 23:45
  • Note that the default `boxplot` call in R has the `range` parameter set to 1.5. This means that the wiskers extend to 1.5 times the interquartile range (see `?boxplot`). The `out` member of the output marks *outliers* in the sense that it marks values that are outside of the wiskers. Change the wiskers range and you will change the limit for outliers. Remove data points and you will most probably change the outliers (as you are changing the IQR). – nico May 09 '13 at 08:43
  • 1
    But why do you want a "more uniform sample"? There are older students. Your sample reflects that. I still see no reason to remove these outliers. – Peter Flom May 09 '13 at 10:31
  • Because I subsequently have to test some subjects in a laboratory setting, so they will take part at a behavioral study. I suspect that it is not good to compare a 18 with a 60 years old subject. – this.is.not.a.nick May 09 '13 at 11:48
  • @this.is.not.a.nick Sadly you didn't post any data. I suspect you're miss-using these boxplots. Have a look at the answers to [this question](http://stats.stackexchange.com/q/13086/603) – user603 May 09 '13 at 20:09

4 Answers4

7

If you have that many outliers, they aren't outliers; you have a non-normal distribution.

How are you going to be using the age variable? One possibility is that it is to be used as an independent variable in a regression. In this case, this distribution is not necessarily a problem - regression makes assumptions about the error (as measured by the residuals) not about the distribution of the independent variables.

(Also, @Doug 's answer is good, and you should tell us that, too).

Peter Flom
  • 94,055
  • 35
  • 143
  • 276
2

Answers 1: maybe, 2: depends. We need a little more information on why you want to remove these outliers. If you could provide a histogram, it might be possible to transform the data and eliminate some of the outliers, but it all depends on the research questions. Please tell us more about 1) your research questions, 2) your participants, and 3O) how you are defining outliers (or are you allowing the boxplots to define them for you).

doug.numbers
  • 833
  • 5
  • 16
-1

when you remove outliers no of data changes thus its quantile changes means lower range and upper range changes thus it is again showing outliers

If you observe both box plot carefully your upper range for first in nearly 38 after removing outlier it become nearly 32

Prashant
  • 1
  • 1
  • 1
    Hello, welcome to CV. Your answer is difficult to read, can you perhaps edit it to be clearer? – Avelina Jul 12 '21 at 15:44
-2

Ok here is what I learned, It is enough to pick out the outliers once from your dataset. If you continue to do so IQR changes respectively which will keep giving you new outliers. If you do not want to see the outliers once you picked them out just add the code, "outline=F", to avoid seeing the new outliers. Hope this helps.

Deepak Bhandari
  • 1
  • What do you mean when you say *"It is enough to pick out the outliers once from your dataset"*?! – Jim Feb 03 '20 at 19:40
  • @Sycorax This post addresses the major thrust of the original question, which appears to concern whether to iterate outlier removal, and it even gives (part of) a good reason not to iterate. – whuber Feb 03 '20 at 20:36
  • @whuber The way it's worded ("Ok, here is what I learned...") lead me to believe that OP was replying to another answer or comment. – Sycorax Feb 03 '20 at 20:43
  • 1
    @Sycorax They are actually following up on a now-deleted post indicating they began with the same problem a few days ago. – whuber Feb 03 '20 at 20:45