would someone please explain why the degrees of freedom for a random sample is n-1 instead of n ?
I'm looking for an explanation that is intuitive and easily understood by a high school student.
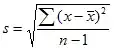
would someone please explain why the degrees of freedom for a random sample is n-1 instead of n ?
I'm looking for an explanation that is intuitive and easily understood by a high school student.
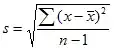
The short answer is that dividing by n returns a biased approximation of the population standard deviation (which is usually what we are trying to estimate from our sample.) Such a calculation for sample standard deviation will be biased low (i.e. an underestimate) relative to the population standard deviation.
Dividing by n-1 makes the sample variance an unbiased estimator, and the sample standard deviation a less biased estimator (this bias is still an issue while n is small.)
Wikipedia provides some details here.
Version 1 ("they complain that the real answer is too hard, so here's some handwaving for non-mathematically-inclined students"):
If you knew the real distribution average, you could construct a sum of squares of independent identically distributed standard normal variables $\xi_i$, similar to $S^2$, and it would've been $\chi_n^2$-distributed: $\frac{(n-1)\hat{S}^2}{\sigma^2} = \sum \limits_{i=1}^{n} (\frac{\xi_i-\mu}{\sigma})^2 \sim \chi^2_n$ with $n$ degrees of freedom.
However, you need to know the real distribution mean $\mu$ and distribution variance $\sigma^2$ to achieve the desired sum, and they are not available in real-life small sample situation.
As you don't know the real distribution mean $\mu$, you have to approximate it with sample average $\bar{\xi}=\frac{\sum \limits_{i=1}^n \xi_i}{n}$.
But this takes away one degree of freedom (if you know the sample mean, then only $\xi_i$ from $1$ to $n-1$ can take arbitrary values, but the $n$th has to be $\xi_n = \hat{\xi} - \sum \limits_{i=1}^{n-1}\xi_i$).
So your real $S^2$ loses one degree of freedom: $\frac{(n-1)S^2}{\sigma^2} = \sum \limits_{i=1}^{n} (\frac{\xi_i-\bar{\xi}}{\sigma})^2 \sim \chi^2_{n-1}$
Oh, and here's a cute kitten for you.
Version 2 ("the real answer, if you do care, as short as I can make it and with as little background required, as possible"):
If you had sum of squares of i.i.d. standard normal variables $\xi_i$, it would've been $\chi_n^2$-distributed: $\sum \limits_{i=1}^{n} (\frac{\xi_i-\mu}{\sigma})^2 \sim \chi^2_n$ with $n$ degrees of freedom.
However, you need to know the real distribution mean $\mu$ and distribution variance $\sigma^2$ to achieve the desired sum that are not available in real-life small sample situation. Your best bet is to use sample average $\bar{\xi}=\frac{\sum \limits_{i=1}^n \xi_i}{n}$ and sample variance $S^2 = \frac{1}{n-1}\sum \limits_{i=1}^n (\xi_i-\bar{\xi})^2$ instead. If you substituted sample mean for the distribution mean, notice that the squares of normal random variables in the sum $\sum \limits_{i=1}^n (\frac{\xi_i-\bar{\xi}}{\sigma})^2$ stop being independent (e.g. if $n=2$ two normal variables $\frac{\xi_1-\hat{\xi}}{\sigma}$ and $\frac{\xi_2-\bar{\xi}}{\sigma}$ are exact opposites of each other, if $\frac{\xi_1-\bar{\xi}}{\sigma} = k$, you know that $\frac{\xi_2-\bar{\xi}}{\sigma} = -k$). Thus you can no longer assume that $\sum \limits_{i=1}^n (\frac{\xi_i-\bar{\xi}}{\sigma})^2$ is chi-square distributed.
Let us find another way to achieve chi-square-distributed random variables. You can express your true sum of independent random variables through the approximate one (add and subtract the sample mean to the numerator of each term of your sum and rearrange):
$\sum \limits_{i=1}^n \frac{(\xi_i - \mu)^2}{\sigma^2} = \sum \limits_{i=1}^n \frac{(\xi_i - \bar{\xi} + \bar{\xi} - \mu)^2}{\sigma^2} = \sum \limits_{i=1}^n (\frac{(\xi_i-\bar{\xi})^2}{\sigma^2} + \underbrace{2 \frac{(\xi_i - \bar{\xi})(\bar{\xi} - \mu)}{\sigma^2}}_{0 \text{ due to }\sum \limits_{i=1}^n (\xi_i - \bar{\xi}) = 0} + \frac{(\bar{\xi} - \mu)^2}{\sigma^2})$
$\sum \limits_{i=1}^n \frac{(\xi_i - \mu)^2}{\sigma^2} = (n-1)\frac{S^2}{\sigma^2} + n\frac{(\bar{\xi} - \mu)^2}{\sigma^2}$, where $\sum \limits_{i=1}^n \frac{(\xi_i - \mu)^2}{\sigma^2} \sim \chi^2_n$, $n\frac{(\bar{\xi} - \mu)^2}{\sigma^2} \sim \chi^2_1$.
$f_{\sum \limits_{i=1}^n \frac{(\xi_i - \mu)^2}{\sigma^2}}(t) = \int \limits_{s=-\infty}^{\infty}f_{(n-1)\frac{S^2}{\sigma^2}}(t-s) \cdot f_{n\frac{(\bar{\xi} - \mu)^2}{\sigma^2}}(s)ds$
$\frac{t^{n/2-1}e^{-t/2}}{\Gamma(n/2)2^{n/2}} = \int \limits_{s=-\infty}^{\infty} f_{(n-1)\frac{S^2}{\sigma^2}}(t-s) \cdot \frac{s^{1/2-1}e^{-s/2}}{\Gamma(1/2)2^{1/2}} ds$.
Suppose that $f_{(n-1)\frac{S^2}{\sigma^2}}(t-s) \sim \chi_{n-1}^2$, then $f_{(n-1)\frac{S^2}{\sigma^2}}(t-s) = \frac{(t-s)^{(n-1)/2-1}e^{-(t-s)/2}}{\Gamma((n-1)/2)2^{(n-1)/2}}$. Substitute it into the integral:
$\frac{t^{n/2-1}e^{-t/2}}{\Gamma(n/2)2^{n/2}} = \int \limits_{s=-\infty}^{\infty} \frac{(t-s)^{(n-1)/2-1}e^{-(t-s)/2}}{\Gamma((n-1)/2)2^{(n-1)/2}} \cdot \frac{s^{1/2-1}e^{-s/2}}{\Gamma(1/2)2^{1/2}} ds = \frac{e^{-t/2}}{2^{n/2} \Gamma((n-1)/2) \Gamma(1/2)} \int \limits_{s=-\infty}^{\infty} (t-s)^{(n-1)/2-1}s^{1/2-1}ds = $
$= \frac{e^{-t/2}}{2^{n/2}\Gamma(n/2)} \int \limits_{s=-\infty}^{\infty} \frac{\Gamma(n/2)}{\Gamma((n-1)/2) \Gamma(1/2)} (t-s)^{(n-1)/2-1}s^{1/2-1}ds$.
Do a variable substitution $s = tu$, $ds = tdu$:
$\frac{e^{-t/2}}{2^{n/2}\Gamma(n/2)} \int \limits_{s=-\infty}^{\infty} \frac{\Gamma(n/2)}{\Gamma((n-1)/2) \Gamma(1/2)} (t-tu)^{(n-1)/2-1}(tu)^{1/2-1}tdu = \frac{t^{n/2-1}e^{-t/2}}{\Gamma(n/2)2^{n/2}} \underbrace{\int \limits_{s=-\infty}^{\infty} (1-u)^{(n-1)/2-1}u^{(1/2-1)}du}_{\beta-\text{distribution integral } =1}$.
Thus, we've shown that $\chi^2_{n-1}(x)$ fits as the distribution of $f_{(n-1)\frac{S^2}{\sigma^2}}(x)$.