8

Background

I have a model with 17 parameters, and I currently use the coefficient of variation ($\text{CV}=\sigma/\mu$) to summarize the prior and posterior distributions of each parameter.

All of the parameters are > 0. I would also like to summarize these pdfs on a normalized scale (in this case standard deviation normalized by the mean) so that they can be compared to each other, and with other statistics presented in similar adjacent plots (sensitivity, explained variance). I will include density plots for each parameter separately, but I would like to summarize them here.

However, the sensitivity of the CV to $\mu$ causes the following confusion that, although easily explained in text, would be preferable to avoid.

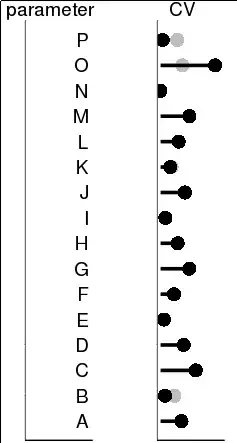
  1. the posterior CV of one parameter is greater than the prior because the mean has decreased more than the variance (parameter O in figure).
  2. one of the parameters (N) is in units of temperature. It has a 95% prior CI of (8,12 Celsius $\simeq$ 281-285K); when I present the data in units of Kelvin which is only defined for positive values, the CV is <1%, if presented as C, the CV is closer to 40%. To me, it seems that neither of these CVs provides an intuitive representation of the CI.

Question

Are there better ways to present this information, either as a CV or as another statistic?

Figure

As an example, this is the type of plot that I am planning to present, with posterior CV in black and prior CV in grey. For scale, the CV of parameter O is 1.6.

alt text

kjetil b halvorsen
  • 63,378
  • 26
  • 142
  • 467
David LeBauer
  • 7,060
  • 6
  • 44
  • 89
  • What assumptions are you making about the distributions? Are they all, for example, lognormal? – whuber Dec 29 '10 at 05:10
  • @whuber each distribution has it's own assumptions, priors are either beta, gamma, logN, or weibull and only six are updated with data; in these cases the posterior distributions are simulated – David LeBauer Dec 29 '10 at 05:51
  • @David Given these distributions come from different families, it seems that CVs will be difficult to interpret and compare among distributions. Could you clarify then why you are tracking the change in CV and how you intend the CVs to be interpreted? – whuber Dec 30 '10 at 15:23
  • @whuber I would like to quantify the amount of information that we have about each parameter before and after adding data. I would like the figure to show something like CV as an index of how well a parameter is constrained, so that this can be compared to sensitivity of the model to the parameter and the contribution of the parameter to model output variance. – David LeBauer Dec 30 '10 at 16:15
  • 1
    If you want to measure the constrain-ness of a parameter, what about to use st.dev(posterior)? If you want to compare constrain-ness of different parameters, what about to use st.dev.(posterior)/st.dev(prior)? – glassy Jan 13 '11 at 14:50
  • "*if presented as C, the CV is closer to 40%*" CV is really only very meaningful as a way of comparing positive (ratio-scale) variables. Temperatures in Celsius have an arbitrary origin and are not positive. If you don't feel that it makes sense to use CV for data in Kelvin *it probably doesn't make sense to use it for that variable at all* – Glen_b Jun 15 '17 at 04:38

2 Answers2

5

It seems to me that CV is inappropriate here. I think you may be better off separating the change in location from the change in dispersion. In addition, the distributions you mention in your comment to the question are, for most parameter values, skewed (positively, except for the beta distribution). That makes me question whether the standard deviation is the best choice for a measure of dispersion; perhaps the interquartile range (IQR) might be better, or possibly the median absolute deviation? Similarly, rather than the mean, I might consider the median or the mode as the measure of location. The choice might in practice be determined by ease of computation as well as the field of application, the details of the model...

Say you choose to use the IQR and the mode. You could summarise the change in dispersion using the ratio of posterior to prior IQRs, probably plotted on a log scale as that's usually appropriate for ratios. You could summarise the change in location using the ratio of the difference between posterior and prior modes to the prior IQR, or to the posterior IQR, or perhaps to the geometric mean of the posterior and prior IQRs.

These are just some quick ideas that came to mind. I can't claim any strong underpinnings for them, or even any great personal attachment to them.

onestop
  • 16,816
  • 2
  • 53
  • 83
  • 1
    I think the robust analogue of CV would be the Winsorized standard deviation divided by the trimmed mean. – shabbychef Dec 30 '10 at 00:08
  • you make a good point about reporting the change in means and the change in variability separately, and your proposed metrics are nice and intuitive. I am going to have to play around with these, and research some of the leads given by @shabbychef before deciding which path to choose, thanks for your answer – David LeBauer Jan 03 '11 at 19:20
5

Some alternatives, which have the same 'flavor' as CV are:

  1. The coefficient of L-variation, see e.g. Viglione. The second sample L-moment takes the place of the sample standard deviation.
  2. The $\gamma$-Winsorized standard deviation divided by the $\gamma$-trimmed mean. You probably want to divide this by $1 - 2\gamma$ to get a consistent scaling across different values of $\gamma$. I would try $\gamma = 0.2$.
  3. The square root of the number of samples times the McKean-Schrader estimate of the standard error of the median, divided by the sample median.
shabbychef
  • 10,388
  • 7
  • 50
  • 93
  • 1
    +1 for mentioning L-moments! Glad i'm not their only proselytizer around here. I'm not convinced that normalizing/standardizing by dividing by a measure of location is the best approach here though, which is why I suggested dividing by a measure of dispersion instead. See point number 2 involving temperature in the question. – onestop Dec 30 '10 at 09:49
  • thanks for these leads, the windsorization approach seems to be the most straightforward, but the L-moments approach also looks promising based on the Vigilone 2010 article, so I will check them out. Can you recommend a good textbook reference? – David LeBauer Jan 03 '11 at 19:22
  • 1
    @David, my favorite text on 'robust statistics' is Wilcox' 'Introduction to Robust Estimation and Hypothesis Testing.' (2nd edition; 3rd ed to appear in July) http://amzn.to/hcpZm2 This text describes trimmed means, the McKean-Schrader estimate, etc, but does not put them together in terms of coefficients of variation. The author has an R package, see http://www-rcf.usc.edu/~rwilcox/ I do not have a good reference on L-CV other than Viglione, but I believe the L-CV is just the Gini coefficient, up to a rescaling. @onestop would know better than I about that. – shabbychef Jan 03 '11 at 19:41
  • @David, Wilcox has a more 'accessible' text, 'Applying Contemporary Statistical Techniques', but I prefer the 'Introduction' text. YMMV. – shabbychef Jan 03 '11 at 19:42