Optimal stopping from an unknown distribution

Question

The Secretary problem has an algorithm for fixed N and immediate accept/reject (that is, reject reject ... accept one, stop). There are several variants; in mine, secretaries or samples come from a real-valued source X_j, payoff is from best-so-far not last, and each sample costs $ c:

maximize payoff = X_bestsofar - c * Nsample

Here's a picture of random walks of this kind: either go up to a high-water mark (new maximum) of X₁ X₂ ..., or down c:

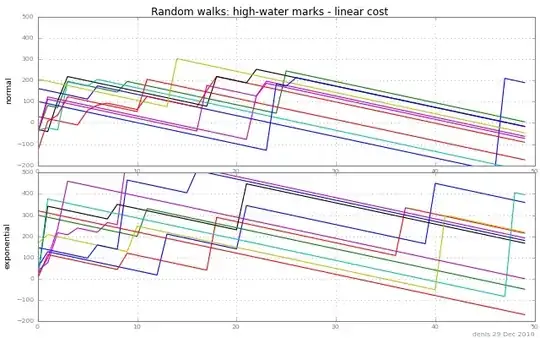
Can anyone point me to stop-or-keep-looking rules for optimal stopping for problems like this ? Perhaps one could combine two kinds of rule:

• sample at least ..., take the best after that (Secretary problem)

• stop when the peak - current exceeds some Δ (Allaart)

As @whuber points out, one needs some model of the distribution of the samples to define the problem. This I don't have. Nonetheless, statisticians must have looked at problems of this kind -- sequential sampling, sequential design of experiments, optimal stopping, optimal learning ? Then please help me rephrase my question to ask for a tutorial on ...

Added links 29Dec, thanks @James; readers please extend —
Optimal stopping
Hill, Knowing when to stop 2009, 3p, excellent
Allaart, Stopping the maximum of a correlated random walk with cost for observation 2004, 12p

(Sorry to keep changing this — trying to converge to a standard formulation.)

Answer 1

Not an answer, but maybe this helps to clarify the question...

I don't think the secretary problem is without dependence on the underlying distribution. For example, if the observations aren't stationary, the 37% approach is not likely to be optimal.

For a concrete example, a person making monthly purchases in an index fund for their retirement account could use the 37% rule to try to buy in at the low of the each month. In practice, this strategy doesn't work well because prices tend to trend upward. If some poster can cite work which deals with optimal stopping rules when the observations display trends, I'd be grateful.

Perhaps a more helpful response to the original question is this paper Skip the Square Root of n: A New Secretary Problem which deals with the objective of maximizing the expected rank of the chosen element, rather than the probability of choosing the top ranked element as in the classical secretary problem.

Answer 2

Also not an answer, but a back-of-the envelope calculation for the simpler case of i.i.d. X_j from a known distribution, to help my (non-statistician's) intuition:

Example Monte Carlo, to show the wide variation in run lengths, payoffs and costs:

# sample exponential*100 until > the first 3
# c0 = break-even cost, peak / n

15  [ 54 127   0  36  16  10  21  42  51  77  54 116  23 210]
17  [24 31 68  5 85]
22  [345  38 118 209 225   9   4  19 210  10  55 317  76 118  38 116 180   2 139 450]
23  [  3 111  54  82  15  22 161]
23  [ 35  34  14   2 114]

24  [ 16  89 120  11  53 119  53   5  77 109  72 289]
33  [ 88 234  15  15 165  51  18 262]
40  [138  33 156  11  59 239]
45  [ 98 139  43  31 226]
54  [ 43 139 129 215]

For X_j i.i.d. from a known distribution, one can calculate the following:

Emax3 = Expected max( X₁ .. X₃ ) # or 10 or √ n ...
p = Prob { X > Emax3 }
Ntopeak ~ 1/p, the expected number of draws to the first X > Emax
Epeak = its expected value

then compare the break-even cost c0 = Epeak / (3 + Ntopeak) to the ante you can afford. For exponentials, as above, I get

expon 3:
Emax3 158
Ntopeak 5
Epeak quartiles [187 227 296]
c0 ~ [187 227 296] / (3 + 5) = [23 28 37]
    # but Epeak dist / Ntopeak dist ?

For a given distribution and cost-per-sample c, one could optimize the number of initial samples (here 3) by brute force. But the high variance in such results makes them hard to communicate, even misleading.