10

Greetings,

I'm performing research that will help determine the size of observed space and the time elapsed since the big bang. Hopefully you can help!

I have data conforming to a piecewise linear function on which I want to perform two linear regressions. There is a point at which the slope and intercept change, and I need to (write a program to) find this point.

Thoughts?

mpiktas
  • 33,140
  • 5
  • 82
  • 138
rhombidodecahedron
  • 2,322
  • 3
  • 23
  • 37
  • 3
    What is the policy on cross-posting? The exact same question was asked on math.stackexchange.com: http://math.stackexchange.com/questions/15214/finding-the-change-point-in-data-from-a-piecewise-linear-function – mpiktas Dec 22 '10 at 17:58
  • What is wrong with doing simple non-linear least squares in this case? Am I missing something obvious? – grg s Dec 23 '10 at 18:45
  • I'd say that the derivative of the goal function with respect to the change point parameter is rather un-smooth – Andre Holzner Jul 27 '12 at 13:09
  • The slope would change so much that a non-linear least squares wouldn't be concise and accurate. What we know is that we have two or more linear models, therefore we should strike to extract those two models. – SmallChess Oct 30 '15 at 06:18

6 Answers6

8

R package strucchange might help you. Look at the vignette, it has a nice overview how to solve similar problems.

mpiktas
  • 33,140
  • 5
  • 82
  • 138
6

If the number of points is not too big, you may try all possibilities. Let's assume that the points are $X_i=(x_i,y_i)$ where $i=1,..,N$. Than, you may loop with $j$ from $2$ to $N-2$ and fit two lines to both $\{X_1,...,X_j\}$ and $\{X_{(j+1)},...,X_N\}$. Finally, you pick $j$ for which the sum of sum of squared residuals for both lines is minimal.

5

This is an (offline) changepoint detection problem. Our previous discussion provides references to journal articles and R code. Look first at the Barry and Hartigan "product partition model," because it handles changes in slope and has efficient implementations.

Community
  • 1
whuber
  • 281,159
  • 54
  • 637
  • 1,101
3

Also the segmented package has helped me with similar problems in the past.

chl
  • 50,972
  • 18
  • 205
  • 364
Misha
  • 1,173
  • 1
  • 11
  • 25
2

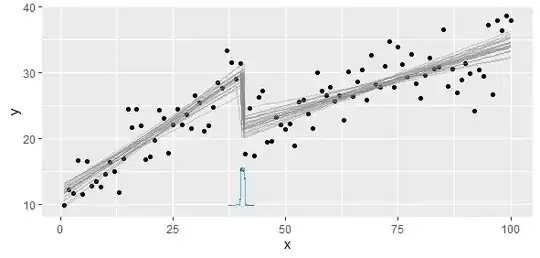
I built on mbq's answer that searching for all the possibilities. Furthermore, I do this:

  • Check for the significance of the two piecewise models to make sure the coefficients are significant
  • Check the difference to the sum of squared residuals for the full model
  • Confirm my model visually (make sure it's not something nonsense)

Why check for the significance? That's because the point with the minimum SSE is meaningless if either of piecewise model fits the data very poorly. This can happen for two highly correlated variables without a clear breakpoint where slopes change.

Let's check this simple approach with an easy test case:

x <- c(-50:50)
y <- abs(x)
plot(x,y,pch=19)

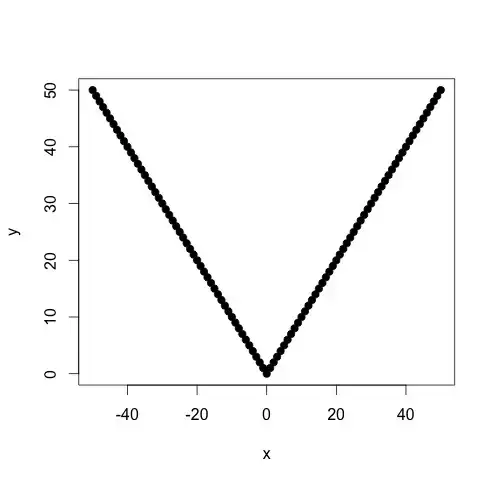
enter image description here

The breakpoint is obviously zero. Use the following R script:

f <- function(x, y)
{
    d <- data.frame(x=x, y=y)
    d <- d[order(x),]
    r <- data.frame(k=rep(0,length(x)-4), sums=rep(0,length(x)-4))

    plm <- function(i)
    {
        d1 <- head(d,i)
        d2 <- tail(d,-i)

        # Make sure we've divided the region perfectly        
        stopifnot(nrow(d1)+nrow(d2) == nrow(d))

        m1 <- lm(y~x, data=d1)
        m2 <- lm(y~x, data=d2)

        r <- list(m1, m2)
        r
    }

    lapply(2:(nrow(d)-3), function(i)
    {
        r$k[i-2] <<- d[i,]$x

        # Fit two piecewise linear models
        m <- plm(i)

        # Add up the sum of squares for residuals
        r$sums[i-2] <<- sum((m[[1]]$residuals)^2) + sum((m[[2]]$residuals)^2)
    })

    b <- r[which.min(r$sums),]    
    b
}

Fit piecewise linear models for all possible combinations:

f(x,y)
   k sums
   0    0

If we check the coefficients for the two optimal models, they will be highly significant. Their R2 will be also very high.

SmallChess
  • 6,764
  • 4
  • 27
  • 48
1

The mcp package can do this. Say your data is

First, let's simulate some data:

df = data.frame(x = 1:100,
                y = c(rnorm(40, 10 + (1:40)*0.5),
                      rnorm(60, 10 + 40*0.5 -8 + (1:60)*0.2)))

Now let's see if we can recover the change point at 40 (and the parameter values) using mcp:

model = list(
  y ~ 1 + x,  # linear segment
  ~ 1 + x  # another linear segment
)
library(mcp)
fit = mcp(model, df)

Plot it. The gray lines are random draws from the fit, showing that it captures the trend. The blue curve is the estimated change point location:

enter image description here

Let's see the individual parameter estimates. int_ are intercepts, x_ are slopes on x, and cp_ are change points:

summary(fit)

Population-level parameters:
    name  mean lower upper Rhat n.eff
    cp_1 40.48 40.02 41.00    1  2888
   int_1 11.12  9.11 13.17    1   778
   int_2 21.72 20.09 23.49    1   717
 sigma_1  3.23  2.76  3.69    1  5343
     x_1  0.46  0.36  0.54    1   724
     x_2  0.21  0.16  0.26    1   754

Disclaimer: I am the developer of mcp.

Jonas Lindeløv
  • 1,778
  • 1
  • 17
  • 28