What hypothesis testing to use for continuous to categorical variables?

Question

For example, I'd like to know if a person's age (a continuous variable) is related to whether the person drinks (a categorical/binary variable of Y or N). What method should I use to know

1. If there's a significant relationship.
2. The strength of the association.
3. The direction of the association - whether younger people tend to drink, or the opposite.

Thanks.

Answer 1

Suppose the ages of $n_1=20$ randomly sampled subjects who drink are $X_i \sim\mathsf{Norm}(\mu = 40, \sigma=7),$ rounded to the next lower year. Independently, suppose ages of $n_2=25$ randomly sample subjects who abstain are $Y_i \sim\mathsf{Norm}(\mu = 30, \sigma=5),$ similarly rounded. Then your data might be similar to the fictitious data sampled in R below:

set.seed(2022)
x = floor(rnorm(20, 40, 7))
y = floor(rnorm(25, 30, 5))

Of course, in a real study, you would not know the population mean and variances. But from the data you could find summary statistics as shown below. This gives the impression that drinkers are often older than abstainers.

summary(x);  length(x);  sd(x)
   Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
  19.70   33.29   39.07   38.05   42.77   47.14 

[1] 20         # size of first sample
[1] 7.002077   # SD of first sample

summary(y)  length(y);  sd(y)
   Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
  22.21   28.26   30.59   30.15   33.25   36.06 
[1] 25
[1] 3.948933

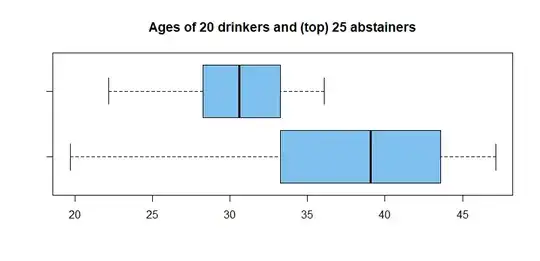
Boxplots (x on bottom) of the two samples are as follows. There are not signs of severe skewness or of many oultiers, so we believe the data are roughly normal. It seems appropriate to do a Welch two-sample t test (which does not assume equal variances) to see if the difference between $\bar X = 38.05$ and $\bar X = 30.15$ is statistcally significant at the 5% level.

hdr="Ages of 20 drinkers and (top) 25 abstainers"
boxplot(x,y, horizontal=T, col="skyblue2", main=hdr)

A printout from t.test in R for these two samples is shown below. The P-value $0.0001 < 0.05 = 5\%$ shows that the null hypothesis is rejected.

t.test(x, y)

        Welch Two Sample t-test

data:  x and y
t = 4.5042, df = 28.441, p-value = 0.0001042
alternative hypothesis: 
 true difference in means is not equal to 0
95 percent confidence interval:
  4.309023 11.488299
sample estimates:
mean of x mean of y 
 38.05252  30.15386 

Of course, your real data might show a difference in the other direction of nor significant difference at all, but the procedures would be the same for nearly-normal data.

A95% confidence interval for difference between the ages of drinkers and abstainers is given in the output above as $(4.3,\, 11.5).$

Answer 2

What to do here would depend also on sample size, you didn't tell us. If sample size is large enough, you can use logistic regression, possible with splining age. That would also allow for a more complicated (nonmonotone) relationship. That is what is proposed at T-tests, manova or logistic regression - how to compare two groups?, which have more details.

Another similar question is Logistic regression or T test?