2

From Wikipedia

Calculate the test statistic $W$ $$ W = \left|\sum_{i=1}^{N_r} [\operatorname{sgn}(x_{2,i} - x_{1,i}) \cdot R_i]\right|, $$the absolute value of the sum of the signed ranks.

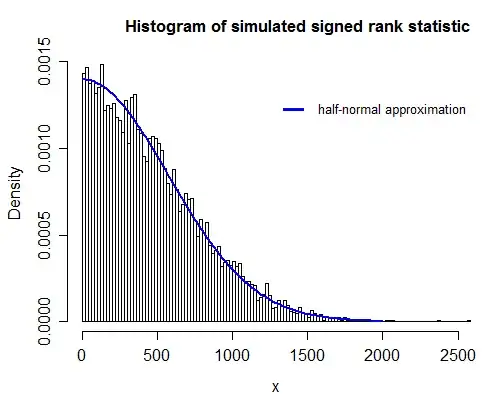
As $N_r$ increases, the sampling distribution of $W$ converges to a normal distribution.

  1. Since $W$ is defined to be always nonnegative, why does the distribution of $W$ converge to a normal distribution which has positive probability of negative values?

    What should it be then?

  2. For $N_r \ge 10$, a z-score can be calculated as $z = \frac{W - 0.5}{\sigma_W}, \sigma_W = \sqrt{\frac{N_r(N_r + 1)(2N_r + 1)}{6}}$.

    Does it mean $E(W) = 0.5$ and $\operatorname{Var}(W) = \frac{N_r(N_r + 1)(2N_r + 1)}{6}$? Why is it true?

Thanks and regards!

Scortchi - Reinstate Monica
  • 27,560
  • 8
  • 81
  • 248
Tim
  • 1
  • 29
  • 102
  • 189
  • The sampling distribution converges to normal although the distribution of W is not normal? The central limit theorem? – Daniel Ezra Johnson Apr 19 '13 at 19:57
  • 3
    There's a subtlety here, Tim, that is obscured by Wikipedia's loose language: $W$ itself will not converge to any distribution at all. In order to converge, it has to be *standardized*, requiring an (infinite) sequence of adjustments. For an illustration and explanation of the distinction please see my answer to a related question at http://stats.stackexchange.com/questions/49123/central-limit-theorem-and-the-law-of-large-numbers/49127#49127. – whuber Apr 19 '13 at 21:01

2 Answers2

3

While a Normal distribution does always include some positive probability of negative values, that probability can be so small as to be meaningless for all intents and purposes.

Height of adult humans is usually thought to be normally distributed. Yet the probability of a height less than 0, while positive, is pretty darn small.

W quickly gets to be very large, so it can get very close to a Normal even if it never actually exactly matches one.

Peter Flom
  • 94,055
  • 35
  • 143
  • 276
  • Thanks! Is it asymptotical normality? It isn't by Central Limit Theorem, because you take absolute value after taking the sum? Then what is it by? – Tim Apr 19 '13 at 19:58
  • Also, note that as $N_r$ increases, the variance $\sigma_W^2$ of the limiting normal distribution also increases, which means that the probability of being negative increases. – Tim Apr 19 '13 at 20:07
  • Because the limiting distribution is achieved only by standardizing the variates, Tim, you *force* all variances to equal $1$ and the variance of the limiting distribution consequently is $1$, also. To make intuitive sense of what's going on you also need to track what's happening to the expectation of $W$: it grows large at a rate sufficient to make the chance of a negative value go to $0$. In some sense, in the limit all negative numbers are "pushed off to $-\infty$" by the standardization procedure. – whuber Apr 19 '13 at 21:03
  • @whuber: Thanks! Can you write down what $W$ is like after being standardized? I don't know how you standardize $W$, but $W$ is not sum, but absolute value of sum, so we cannot apply CLT here, can we? If not, what theorem makes "standardized" $W$ has a normal distribution? – Tim Apr 19 '13 at 21:18
3

Actually, I suspect Wikipedia may be wrong there. That doesn't match the links for starters. That statistic makes me worry for several reasons. The expected value of the sum of the signed ranks of absolute differences will be zero under the null, and a suitably scaled version of it will converge to normality by the CLT. As such, the absolute value of that won't converge to normality, but may, when suitably scaled, converge to a standard half-normal.

Edit:

Having just simulated the distribution under the null at various sample sizes, it looks like I am right - taking the absolute value of the whole thing makes something that would be asymptotically normal become half-normal.

I agree - Wikipedia is wrong when it says that statistic converges to normality. It doesn't look like it does, and I don't recall ever having seen the statistic written that way before.

Later edit:

I should show rather than tell: here's an example simulation using the statistic as defined at the Wikipedia page. I did 10000 simulations of signed rank statistics for a continuous distribution symmetric about 0 (representing the differences), at n=100:

enter image description here

Glen_b
  • 257,508
  • 32
  • 553
  • 939
  • Thanks, Glen_b! What should it be in Wikipedia then? Define $W$ without taking absolute value, and now its null distribution is still the same as what Wikipedia said? – Tim Apr 20 '13 at 12:10
  • Also Matlab signrank function seems to take absolute value too, see discussion [here](http://stackoverflow.com/a/16090333/156458). – Tim Apr 20 '13 at 13:03
  • @Tim There's actually no problem with taking the absolute value of the whole thing (at least if you don't care about one tailed tests), the only problem is claiming it to then be normal; if you work with it being half-normal, everything works fine. To make Wikipedia right and fit with all the other bits and pieces takes more than one simple change - if all it took was removing the absolute value signs I'd have already discussed it on the talk page there and made the edit myself. It's more complex - you have to check it matches the references, and all the discussion that relates to it. – Glen_b Apr 20 '13 at 23:49
  • 1
    While I've fixed pages before, here the task of making sure it's right would require a fair level of effort and constitute such a major change that I wouldn't want to do it without some other knowledgeable people agreeing to check it. However, the typical standard of conversation on that particular wikipedia talk page is so low that I wouldn't want to rely on the denizens of that talk page at all - any error I made could linger indefinitely. I find myself in a dilemma, then. I plan to post something to the talk page about this when I work out what to say, but I doubt it will do any good. – Glen_b Apr 20 '13 at 23:58