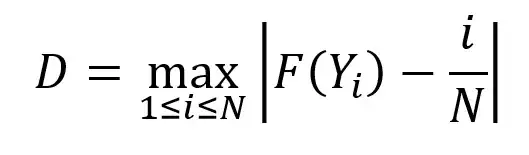I have simulated failure time data for some components.
I tested whether a Weibull or lognormal distribution best fit the data. Please see Figures below. The figures provide median and $95\%$ prediction intervals in black. The green lines are the non-parametric fit (observations).
It looks like the Weibull distribution fits poorly at the lower tail compared to the lognormal distribution. That is, the Weibull fit overestimates the probability of failing at times lower than (approximately) 45.
I think, from a visual check alone, that the lognormal fit is best.
However, I am interested in the lower tail of the failure time distribution, and I believe the lognormal distribution is too optimistic. For example, a $95\%$ prediction interval for the $0.001\%$ quantile under the lognormal model is $[22.5,30.2]$, compared to $[6.4,15.0]$ under the Weibull model.
My understanding is the both the Weibull and the lognormal distributions are heavy-tailed distributions but the tails of the Weibull fit are "much heavier" in the simulation I have performed.
I have also read (no references at hand, sorry) that the lognormal distribution can provide estimates that are too optimistic (in this case predicting that the $0.001\%$ quantile is much higher than it actually is).
The biggest error in my decision problem would be a component failing when I claim that it will not fail. For example, if a component fails after I state the components are unlikely to fail during a 15 hour mission. Therefore, I would like a conservative estimate for the $0.001\%$ quantile.
These reasons could suggest the Weibull model would be best for my problem. However, I think these estimates are too conservative (and wrong) because the model fits poorly in the region I am most interested in.
Is there a way I can "add more uncertainty" in the lognormal fit? Any other suggestions about my problem?